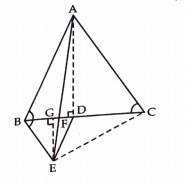
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that :
ar(BFE) = 2ar(FED)Solution in Punjabi
Step by step video & image solution for ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE interesects BC at F, show that : ar(BFE) = 2ar(FED) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
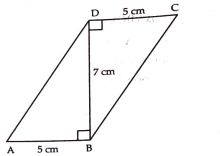 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_E05_020_Q01.png" width="80%"gt
View SolutionIn the given fig. If DE||BC Find EC.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/MATH_241_X_SQP_E01_021_Q01.png" width="80%"gt
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/4 ar( Delta ABC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BDE) = 1/2 ar( Delta BAE)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta ABC) = 2 ar( Delta BEC)
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that ar( Delta BFE) = 2 ar( Delta FED)
View Solution
