△ABC~△PQR. If ar(ABC)=2.25m2.ar(PQR)=6.25m2,PQ=0.5m, then length of AB isSolution in Punjabi
30 cm
1.5 cm
50 cm
2 m
Step by step video & image solution for triangleABC~ trianglePQR. If ar(ABC) = 2.25 m^2. ar(PQR) = 6.25m^2,PQ = 0.5 m, then length of AB is by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
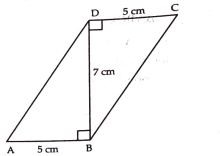 Calculate the area of ||gm ABCD.View Solution
Calculate the area of ||gm ABCD.View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
02:41View SolutionP और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य बिंदु है तथा R रेखाखण्ड AP का मध्य बिंदु है |दर्शाइए
(i)ar(PQR)=12ar(ARC)
(ii)ar(RQC)=38ar(ABC)02:22View SolutionPerimeter of two equilateral triangles ABC and PQR are 144 m and 96 m, Find ar (△ABC):ar(△PQR).
03:17View SolutionGiven △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
01:25View SolutionIn △PQR,∠Q=90∘, PQ=5 cm and PR=13 cm. Then ar(PQR)=____ cm2
02:06View SolutionIn △ABC , P,Q and R are the midpoints of AB, BC and CA respectively. If ar(ABC)=32 cm2 , then ar(PQR)= ____cm2
02:17View SolutionIn △ABC , P, Q and R are the midpoints of AB, BC and CA respectively . If ar(ABC)=____40 cm2, then ar(PBCR)= ____cm2
07:03View SolutionIn △ABC , P, Q and R are the midpoints of AB, BC and CA respectively . If ar(PBQR)=36 cm2 , then ar(ABC)=____ cm2
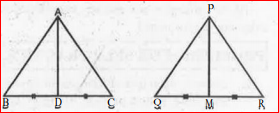
04:32View SolutionIf AD and PM are medians of triangles ABC and PQR, respectively where △ABC~△PQR , Prove that ABPQ=ADPM .
 .05:41View Solution
.05:41View Solution△ABC−△PQR, in △ABC, AB - 5.4 cm, BC = 4.2 cm, AC = 6.0 cm, AB: PQ = 3:2 Construct △ABC and △PQR
03:23View SolutionIf AD and PM are medians of triangles ABC and PQR,respectively where △ABC~△PQR,prove thatABPQ=ADPM.
02:32View SolutionAgreed triangleABC-triangleQPR And (ar(triangleABC))/( ar(trianglePQR) =4/25. If AB=12 cm, BC=8 cm. and AC=9 cm. then PR is equal to
03:23View SolutionLet triangleABC ~ triangleQPR and (ar(triangleABC))/(ar(trianglePQR))=9/16 . If AB=12 cm, BC=6 cm and AC=9 cm then QR is equal to :
02:59View SolutionIn triangleABC , it L and M are points on AB and AC respectively such that LM||BC. Prove that : ar(triangleLCM) = ar(triangleLBM)
04:49View SolutionIn triangleABC , it L and M are points on AB and AC respectively such that LM||BC. Prove that : ar(triangleLBC) = ar(triangleMBC)
02:13View Solution

