Tick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratioSolution in Punjabi
2:3
4:9
81:16
16:81
Step by step video & image solution for Tick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
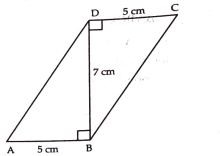 Calculate the area of ||gm ABCD.02:42View Solution
Calculate the area of ||gm ABCD.02:42View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
01:27View SolutionIf the ratio of the sides of two similar triangles be 4:9, then ratio of areas will be
02:22View SolutionThe sides of two similar triangles are 4 : 9 . What is the ratio of their area?
01:17View SolutionThe perimeter of two similar triangles are in 4:9 ratio, the ratio of their corresponding sides is…………..
01:59View SolutionSides of two similar triangles are in the ratio 4 : 9 Areas of these triangles are in the ratio
01:39View SolutionTick the correct answer and justify: Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2:3 (B) 4:9 (C) 81:16 (D) 16:8102:45View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
01:29View SolutionThe side of two similar triangles are 4:9. What is the ratio of their area?
03:03View Solutionਦੋ ਸਮਰੂਪ ਤ੍ਰਿਭੁਜਾਂ ਦੀਆਂ ਭੁਜਾਵਾਂ 4:9 ਦੇ ਅਨੁਪਾਤ ਵਿਚ ਹਨ। ਇਨ੍ਹਾਂ ਤ੍ਰਿਭੁਜਾਂ ਦੇ ਖੇਤਰਫਲਾਂ ਦਾ ਅਨੁਪਾਤ ਹੈ:
02:50View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
03:03View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio___
01:06View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
02:05View SolutionCalculate the ratio of the area of two similar triangles if the sides of the triangles are in the ratio of 9:4.
03:16View SolutionThe ratio of areas of two similar triangles is 4:9. Then, the ratio of their sides is:
View SolutionSides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
02:28View Solution

