If the medians of a △ABC intersect at G, show that ar(AGB)=ar(AGC)=ar(BGC)=1/3ar(ABC)Solution in Punjabi
Step by step video & image solution for If the medians of a triangleABC intersect at G, show that ar(AGB) = ar(AGC) = ar(BGC) = 1/3ar(ABC) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
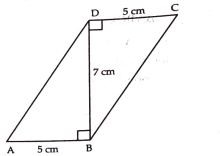 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionIn a ABC,E is the mid-point of median AD. Show that ar(BED)=14ar(ABC)
View SolutionΔABC में, E मध्यिका AD का मध्य - बिंदु है । दर्शाइए कि ar(BED)=14ar(ABC) है।
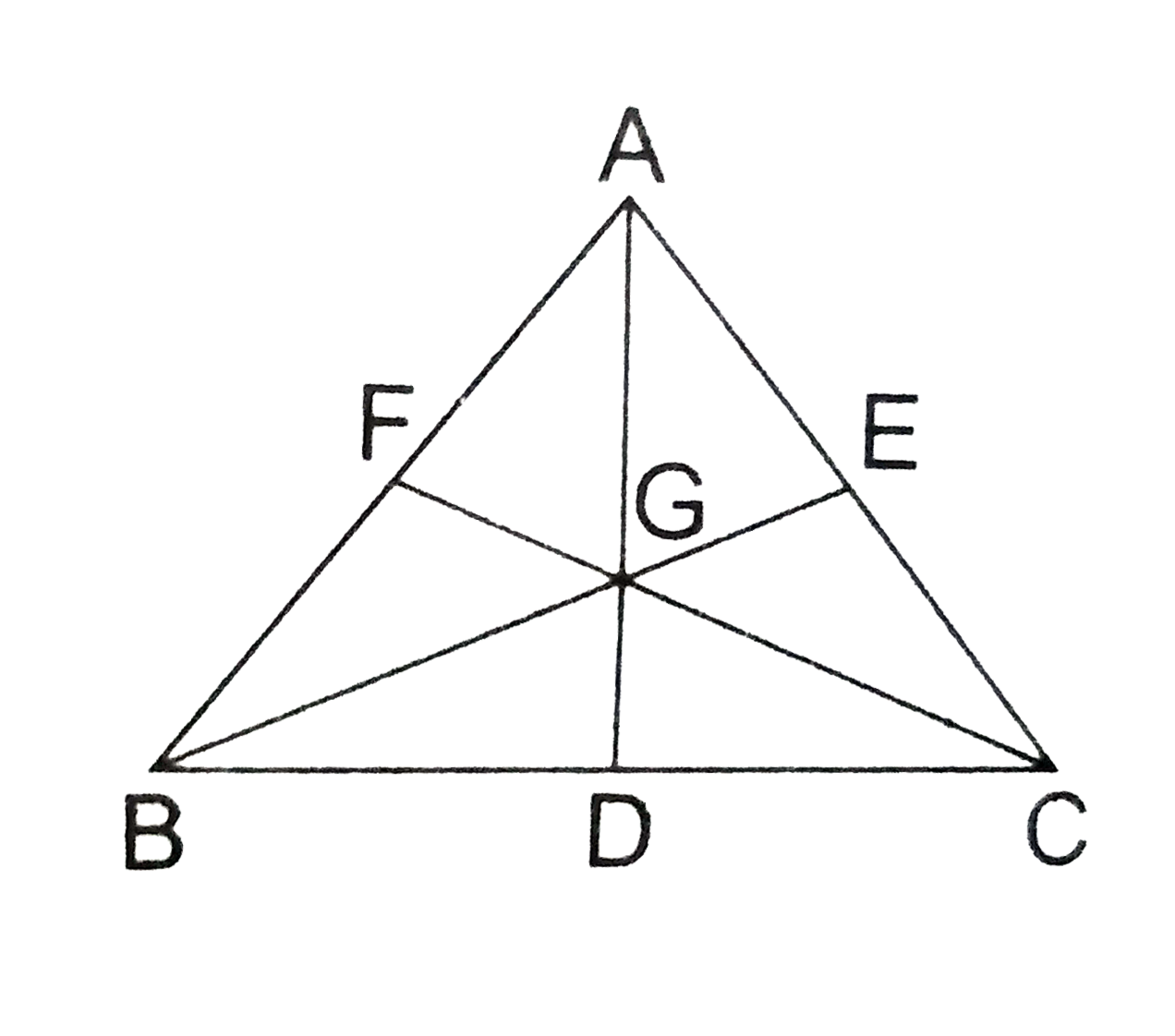
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View Solutionयदि ΔABC की माध्यिकायें बिंदु G पर प्रतिच्छेद करती है, तो सिद्ध कीजिए कि
ar(ΔAGB)=ar(ΔAGC)=ar(ΔBGC)=13ar(ΔABC)
View Solutionयदि त्रिभुज ABC की माध्यिकाएँ बिंदु G पर काटती है तथा
ar(ΔABC)=27 वर्ग सेमी, ar(ΔBAG)=
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = 14 ar (ABC).
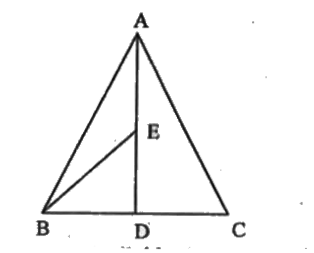
View SolutionIn a triangle ABC, E is the mid - point of median AD. Show that ar (BED) =1/4 ar (ABC)
View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
View SolutionIn a triangle ABC , E is the midpoint of median AD. Show that ar(BED) =14ar(ABC)

View SolutionIn △ABC, AD is a median . E is the midpoint of AD and F is the midpoint of AE. Prove that ar(ABF)=18ar(ABC).
View SolutionIn △ABC, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=12ar(ABC)
View SolutionIf the medians of a triangle ABC meet at G, prove that ar (AGB) = ar (AGC) = ar (BGC) = (1)/(3) is ar (ABC).
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (triangleBED)=1/4 ar( triangleABC ).
View Solution
