ABC is an isosceles triangle in which AB = AC. If D and E are the mid-points of AB and respectively, prove that B,C,D and E are concyclic.Solution in Punjabi
Step by step video & image solution for ABC is an isosceles triangle in which AB = AC. If D and E are the mid-points of AB and respectively, prove that B,C,D and E are concyclic. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - MODERN PUBLICATIONCHAPTER - CIRCLESEXERCISE - EXERCISE
94 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - MODERN PUBLICATIONCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE
83 Videos
- CONSTRUCTIONSBOOK - MODERN PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE
69 Videos
Similar Questions
The radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionIn the figure. Show that ABCD is a parallelogram.
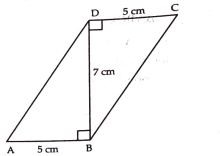 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionDraw a line segment of length 7.3 cm using a ruler.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionDandE are points on equal sides ABandAC of an isosceles triangle ABC such that AD=AE . Prove that B,C,D,E are concylic.
View SolutionIn Figure, ABC is a triangle in which AB=AC. Point DandE are points onthe sides ABandAC respectively such that AD=AE. Show that the points B,C,EandD are concyclic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionD and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD=AE. Prove that B, C, D, E are concyclic.
View SolutionIf in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
View SolutionΔABC एक समद्विबाहु त्रिभुज है जिसमे AB = AC है । यदि D व E क्रमश: भुजाओ AB व AC के मध्य-बिन्दु हो, तो सिध्द करो कि बिन्दु B, C, D व E एक वृतीय होंगे ।
View Solutionएक समद्विबाहु त्रिभुज ABC कि समान भुजाओ AB तथा AC पर बिन्दु D तथा E इस प्रकार हैं कि AD = AE हैं । सिध्द करो कि B, C, D तथा E एक वृतीय होंगे ।
View SolutionABC is an equilateral triangle. D and E are the mid-points of AB and AC. Then ∠ADE=
View SolutionB is a vertex of the isosceles triangle ABC. D and E are the mid-points of AB and AC. If BE and CD intersects each other at F prove that ΔBDE=3ΔDEF.
View Solutionएक समद्धिबाहू त्रिभुज ABC में AB-=AC हों एंव भुजा BC, AC एंव AB के मध्य बिन्दु क्रमश: D, E, F हों तो सिद्ध कीजिए कि DE -= DF
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, Prove that the points B, C, D and E are concyclic.
View Solution
