What is the speed of the body moving with uniform accelerated motion at midpoint of two points on the straight line, where the speeds are u and v respectively?
Let “a” be the constant acceleration. And s be the distance between the two points,
From equation of motion
v2−u2=2as .........(1)
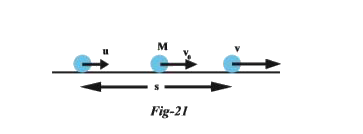
Let v0 be the speed of the body at midpoint ‘M’ of the given points.
Applying the same equation used above, we get
v20−u2=2as/2
From (1),
v20−u2=v2−u22
After some algebra we get,
v0=√v2+u22
Similar Questions
Knowledge Check
For a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
A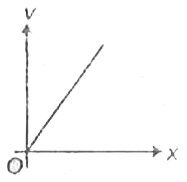 B
B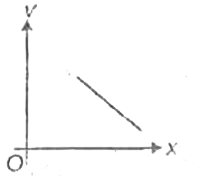 C
C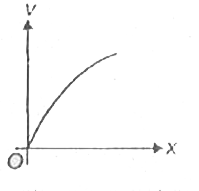 D
D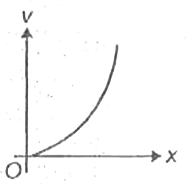
Assertion : The displacement-time graph of a body moving with uniform acceleration is a straight line.
Reason : The displacement is proportional to time for uniformly accelerated motion.AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is false.DIf the assertion and reason both are falseA body is revolving with a uniform speed v in a circle of radiusr . The tangential acceleration is
AvrBv2rCZeroDvr2
Relative speed of two persons moving with u m/s and v m/s in opposite direction where u>v
View SolutionTwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
View SolutionIf a body is moving with a uniform speed v in a circle of radius 'r', then the angular acceleration of the body will be
View SolutionTwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
View SolutionTwo particles A and B are moving in uniform circular motion in concentric circles of radii rA and rB with speed uA and uB respectively. Their time period of rotation is the same. The ratio of angular speed of a to that of B will be:
View Solution
