Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
Evaluate x, by considering the figure below.
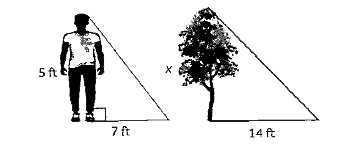
Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day. Evaluate x, by considering the figure below.

A

12 ft

B

15 ft

C

10 ft

D

7 ft

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day. Evaluate x, by considering the figure below. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023
Class 10MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
    Evaluate for x
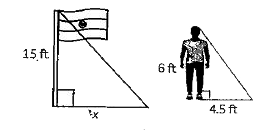    ocr_image

    A10.5 ft
    B11.25 ft
    C12 ft
    D9 ft

  • Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
    What is the height of the tree i.e. h ?
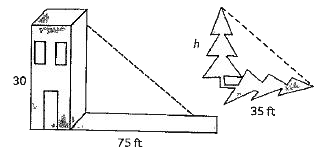    ocr_image

    A20 ft
    B12 ft
    C18 ft
    D14 ft

  • Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
    See the figure below and evaluate the height of the tree.
    If the shadows of a lamp-post and a at the same time of a days are 18 ft. and 6 ft. respectively then what is the height of the lamp-post.
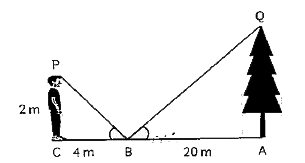    ocr_image

    A25 m
    B40 m
    C20 m
    D10 m