Two triangles are similar if their corresponding sides are ………….
The correct Answer is:Proportional (by definition)
To solve the question "Two triangles are similar if their corresponding sides are ………….," we can follow these steps:
1. Understanding Similar Triangles:
- Similar triangles are triangles that have the same shape but may differ in size. This means that their angles are equal, and their sides are in proportion.
2. Identifying Corresponding Sides:
- Corresponding sides are the sides of the triangles that are in the same relative position. For example, if triangle ABC is similar to triangle DEF, then side AB corresponds to side DE, side BC corresponds to side EF, and side CA corresponds to side FD.
3. Establishing the Relationship:
- For two triangles to be similar, the lengths of their corresponding sides must have a specific relationship. This relationship is that the ratios of the lengths of the corresponding sides must be equal.
4. Conclusion:
- Therefore, we can complete the statement: "Two triangles are similar if their corresponding sides are proportional."
Final Answer:
Two triangles are similar if their corresponding sides are proportional.
---
- Similar triangles are triangles that have the same shape but may differ in size. This means that their angles are equal, and their sides are in proportion.
- Corresponding sides are the sides of the triangles that are in the same relative position. For example, if triangle ABC is similar to triangle DEF, then side AB corresponds to side DE, side BC corresponds to side EF, and side CA corresponds to side FD.
- For two triangles to be similar, the lengths of their corresponding sides must have a specific relationship. This relationship is that the ratios of the lengths of the corresponding sides must be equal.
- Therefore, we can complete the statement: "Two triangles are similar if their corresponding sides are proportional."
Two triangles are similar if their corresponding sides are proportional.
Topper's Solved these Questions
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - VERY SHORT QUESTIONS
10 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-I) TYPE QUESTIONS
30 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos
Similar Questions
Write the truth value (T/F) of each of the following statements: (1)Two polygons are similar if their corresponding angles are proportional. (2)Two triangles are similar if their corresponding sides are proportional. (3) Two triangles are similar if their corresponding angles are proportional.
View SolutionFill in the blanks using the correct word given in brackets: Two triangles are similar, if their corresponding angles are ...... (proportional, equal) Two triangles are similar, if their corresponding sides are ....... (proportional, equal) (iii) Two polygons of the same number of sides are similar, if (a) their corresponding angles are and (b) their corresponding sides are ........ (equal, proportional).
View Solution
Knowledge Check
Magnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
What is the height of the tree i.e. h ?
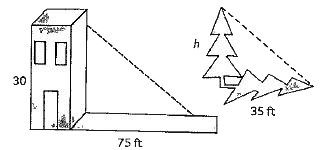 A20 ftB12 ftC18 ftD14 ft
A20 ftB12 ftC18 ftD14 ftMagnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
Evaluate x, by considering the figure below.
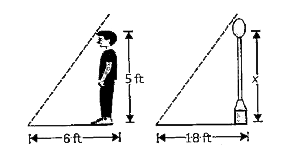 A15 ftB10 ftC12 ftD18 ft
A15 ftB10 ftC12 ftD18 ftMagnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
Evaluate x, by considering the figure below.
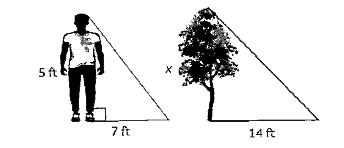 A12 ftB15 ftC10 ftD7 ft
A12 ftB15 ftC10 ftD7 ft
Two polygons of the same number of sides are similar, if their corresponding angles are …………….. . (equal, proportional)
View SolutionThe ratio of the area of two similar triangle is 4:5, the ratio of their corresponding sides are :
View SolutionMagnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
Evaluate for x
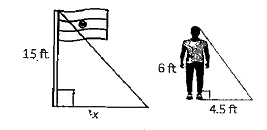
View SolutionMagnification of figures is a process of enlarging the apparent size, not the physical size, of something. The enlarged figure is quantified by a calculated number. If two triangles are similar then their corresponding sides are in the same ratio. Basically a bigger triangle is a enlargement of the smaller triangle. This basic rule of similar triangles is applicable in solving many real life problems like relating the height and shadow length of various objects at a particular instant in a day.
See the figure below and evaluate the height of the tree.
If the shadows of a lamp-post and a at the same time of a days are 18 ft. and 6 ft. respectively then what is the height of the lamp-post.
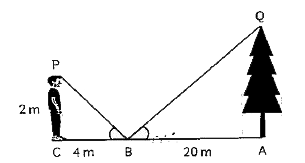
View SolutionAssertion : If the areas of two similar triangles are equal , they are congruent .
Reason : Area of similar triangles are proportiona to their corresponding sides .
View Solution
