In a circuit a metal filament lamp is connected in series with a capacitor of capacitance CμF across a 200V 50Hz supply. Power consumed by lamp is 500W while voltage drop across it is 100V. Assume tht there is no inductive load in the circuit . Take rms values of the voltages . The magnitude of the phase angle between current and supply voltage is ψ. Value of ψ is
To solve the problem, we need to find the phase angle ψ between the current and the supply voltage in a circuit consisting of a metal filament lamp and a capacitor connected in series.
1. Given Data:
- Power consumed by the lamp, P=500W
- Voltage drop across the lamp, VR=100V
- Supply voltage, V=200V
- Frequency, f=50Hz
2. Calculate Resistance of the Lamp:
The power consumed by the lamp can be expressed as:
P=V2RR
Rearranging gives:
R=V2RP=1002500=10000500=20Ω
3. Calculate Current through the Circuit:
Using Ohm's Law:
I=VRR=10020=5A
4. Calculate Total Impedance:
The total voltage across the circuit is given as V=200V. The total impedance Z can be calculated using:
V=I⋅Z⟹Z=VI=2005=40Ω
5. Calculate Capacitive Reactance:
The total impedance in a series circuit with resistance R and capacitive reactance XC is given by:
Z=√R2+X2C
Substituting the known values:
40=√202+X2C
Squaring both sides:
1600=400+X2C⟹X2C=1200⟹XC=√1200=20√3Ω
6. Calculate Capacitance:
The capacitive reactance is given by:
XC=1ωCwhereω=2πf=100π
Thus:
20√3=1100πC⟹C=120√3⋅100π=12000π√3≈100μF
7. Calculate Phase Angle ψ:
The phase angle ψ can be calculated using:
tanψ=XCR=20√320=√3
Therefore:
ψ=tan−1(√3)=60∘
Final Answer:
The magnitude of the phase angle ψ is 60∘.
- Power consumed by the lamp, P=500W
- Voltage drop across the lamp, VR=100V
- Supply voltage, V=200V
- Frequency, f=50Hz
The power consumed by the lamp can be expressed as:
P=V2RR
Rearranging gives:
R=V2RP=1002500=10000500=20Ω
Using Ohm's Law:
I=VRR=10020=5A
The total voltage across the circuit is given as V=200V. The total impedance Z can be calculated using:
V=I⋅Z⟹Z=VI=2005=40Ω
The total impedance in a series circuit with resistance R and capacitive reactance XC is given by:
Z=√R2+X2C
Substituting the known values:
40=√202+X2C
Squaring both sides:
1600=400+X2C⟹X2C=1200⟹XC=√1200=20√3Ω
The capacitive reactance is given by:
XC=1ωCwhereω=2πf=100π
Thus:
20√3=1100πC⟹C=120√3⋅100π=12000π√3≈100μF
The phase angle ψ can be calculated using:
tanψ=XCR=20√320=√3
Therefore:
ψ=tan−1(√3)=60∘
The magnitude of the phase angle ψ is 60∘.
Topper's Solved these Questions
Similar Questions
In a circuit a metal filament lamp is connected in series with a capacitor of capacitance CμF across a 200V 50Hz supply. Power consumed by lamp is 500W while voltage drop across it is 100V. Assume tht there is no inductive load in the circuit . Take rms values of the voltages . The magnitude of the phase angle between current and supply voltage is ψ. Value of C is
View SolutionA coil is series with a 20μF capacitor across a 230V,50Hz supply. The current taken by the circuit is 8A and the power consumed is 200W. Calculate the inductance of the coil if the current in the circuit is
(a) leading
(b) lagging
View Solution
Knowledge Check
In series LCR circuit, the phase angle between supply voltage and current is
Atanϕ=XL−XCRBtanϕ=RXL−XCCtanϕ=RXL+XCDtanϕ=XL+XCRIn an AC circuit , an alternating voltage e = 200sin 100t V is connected to a capacitor of capacity 1μF . The rms value of the current in the circuit is
A100 mAB200 mAC20 mAD10 mAA circuit has a coil of resistance 60 ohm and inductance 3 henry. It is connected in series with a capacitor of 4μF and A.C supply voltage of 200V and 50 cycle/sec
Athe impedance of the coil is 943ΩBthe impedance of the coil is 843ΩCthe p.d. across the inductor coil is 1110VDthe p.d. across the capacitor is 924V
A capacitor of capacitance 10μF is connected to a 220 V , 30 Hz alternating current source . Calculate the peak value of voltage across the capacitor . Also calculate the rms value of current in the circuit .
View SolutionIn an RC series circuit connected across and AC source of 150 V 70 Hz, the value of R is 820 Ω and voltage across it is 100V. Calculate the voltage drop across capacitor connected in series.
View SolutionA resistor and a capacitor are connected to an ac supply of 200 V, 50 Hz, in series. The current in the circuit is 2A. If the power consumed in the circuit is 100 W then the resistance in the circuit is
View SolutionAn alternating voltage is connected in series with a resistance R and inductance L if the potential drop across the resistance is 200V and across the inductance is 150V, then the applied voltage is
View SolutionIn a series C−R circuit shown in figureure, the applied voltage is 10V and the voltage across capacitor is found to8V. The voltage across R, and the phase difference between current and the applied voltage will respectively be
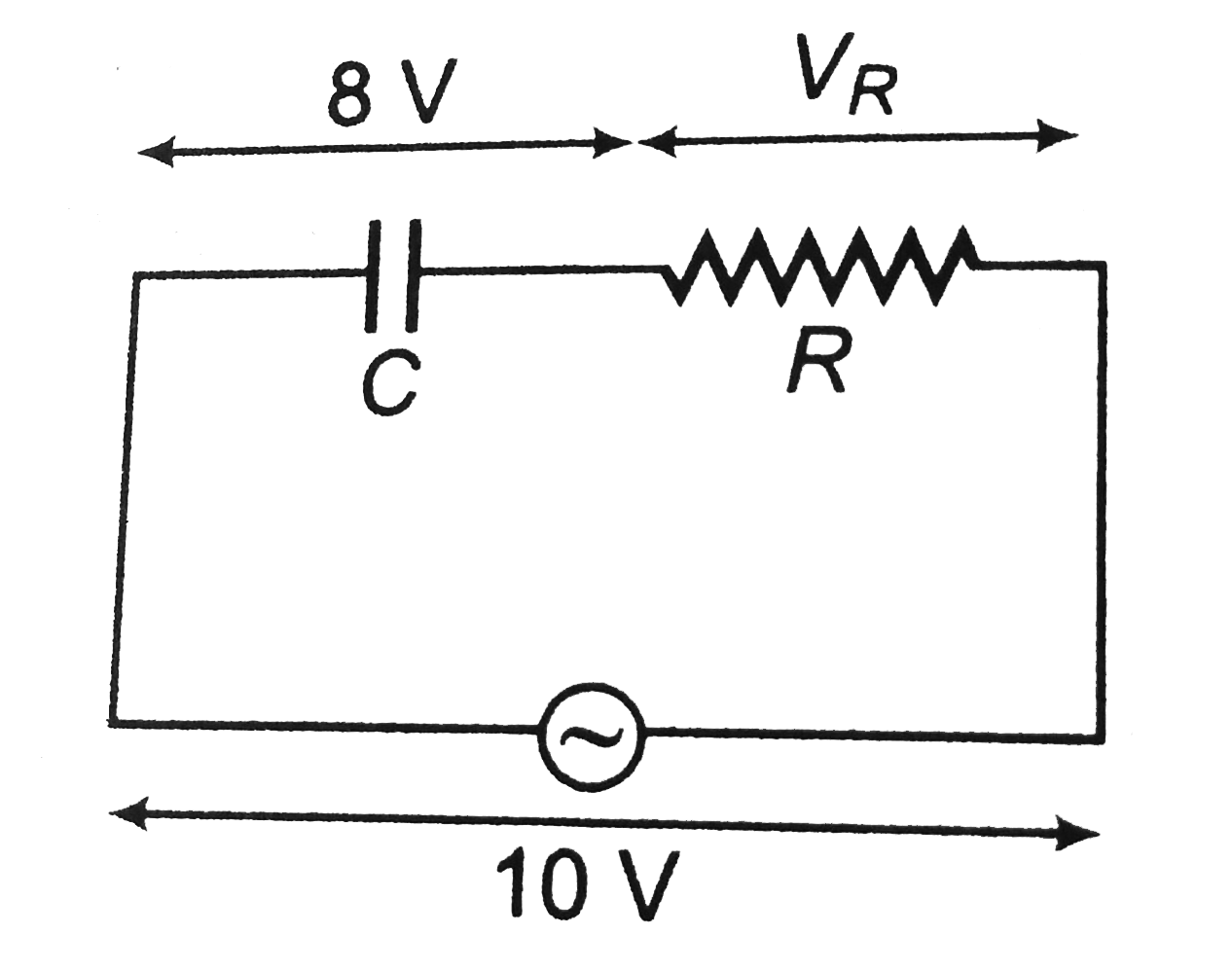 .
.
View Solution