A pendulum consists of a bob of mass m=0.1kg and a massless inextensible string of length l=1.0m. It is suspended from a fixed point at height h=0.9m above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse P=02.kg−m/s is imparted to the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is J kg-m2/s. The kinetic energy of the pendulum just after the lift-off js K Joules.
The value of J is ___
To solve the problem, we need to find the magnitude of the angular momentum J of the pendulum about the point of suspension just before the bob lifts off.
1. Understanding the System:
- The mass of the bob m=0.1kg.
- The length of the string l=1.0m.
- The height of the point of suspension above the floor h=0.9m.
- An impulse P=0.2kg m/s is imparted to the bob.
2. Finding the Velocity of the Bob:
- The impulse given to the bob changes its momentum. The change in momentum is equal to the impulse:
P=m⋅v⟹v=Pm
- Substituting the values:
v=0.2kg m/s0.1kg=2m/s
3. Calculating the Angular Momentum:
- The angular momentum L about the point of suspension just before the bob lifts off can be calculated using the formula:
L=m⋅v⋅r
- Here, r is the perpendicular distance from the line of action of the velocity to the pivot point. Since the bob is at height h=0.9m, the perpendicular distance r is equal to this height.
- Thus, substituting the values:
L=m⋅v⋅h=0.1kg⋅2m/s⋅0.9m
- Calculating L:
L=0.1⋅2⋅0.9=0.18kg m2/s
4. Final Answer:
- Therefore, the value of J is:
J=0.18kg m2/s
- The mass of the bob m=0.1kg.
- The length of the string l=1.0m.
- The height of the point of suspension above the floor h=0.9m.
- An impulse P=0.2kg m/s is imparted to the bob.
- The impulse given to the bob changes its momentum. The change in momentum is equal to the impulse:
P=m⋅v⟹v=Pm
- Substituting the values:
v=0.2kg m/s0.1kg=2m/s
- The angular momentum L about the point of suspension just before the bob lifts off can be calculated using the formula:
L=m⋅v⋅r
- Here, r is the perpendicular distance from the line of action of the velocity to the pivot point. Since the bob is at height h=0.9m, the perpendicular distance r is equal to this height.
- Thus, substituting the values:
L=m⋅v⋅h=0.1kg⋅2m/s⋅0.9m
- Calculating L:
L=0.1⋅2⋅0.9=0.18kg m2/s
- Therefore, the value of J is:
J=0.18kg m2/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
AmL√2gLBmL√gLCmL√3gLDnone
A bob of mass m connected to the end of an inextensible string of length l, is released from position shown in figure. If impacts of bob with smooth floors is perfectly inelastic. Choose the correct options (s)AThe maximum height reached by the bob during subsequency motion is l32BMaximum height reached by the bob during subsequency motion is zero.CEnergy loss from the time duration bob is released to the time it reaches at its maximum height during subsequent motion is 3mgl8DEnergy loss from the time duration bob is released to the time it reaches to the time it reaches at its maximum height during subsequency motion is 15mgl32
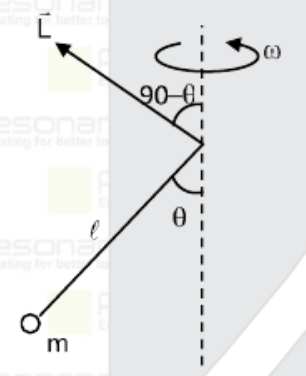
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionA bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View Solution
A simple pendulum consists of a bob of mass m and a light string of length l as shown in the fig. another identical ball moving with the small velocity v0 collides with the pendulum's bob and sticks to it. For this new pendulum of mass 2 m, mark out the correct statements (s).
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View Solution