A pendulum consists of a bob of mass m=0.1kg and a massless inextensible string of length l=1.0m. It is suspended from a fixed point at height h=0.9m above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse P=02.kg−m/s is imparted to the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is J kg-m2/s. The kinetic energy of the pendulum just after the lift-off js K Joules.
The value of K is ___
To solve the problem, we need to find the kinetic energy K of the pendulum just after the lift-off. We will follow these steps:
Step 1: Determine the velocity of the bob after the impulse
The impulse P given to the bob is 0.2kg m/s. The mass m of the bob is 0.1kg. The velocity V of the bob after the impulse can be calculated using the formula:
V=Pm
Substituting the values:
V=0.2kg m/s0.1kg=2m/s
Step 2: Analyze the geometry of the pendulum
When the bob lifts off, it forms an angle θ with the vertical. The height h from which the bob is suspended is 0.9m and the length of the string l is 1.0m.
Using the right triangle formed by the vertical height and the string, we can find cosθ:
cosθ=hl=0.9m1.0m=0.9
Step 3: Resolve the velocity into components
The velocity V can be resolved into two components:
- Along the string: Vcosθ
- Perpendicular to the string: Vsinθ
Since the component along the string does not contribute to the kinetic energy after lift-off, we only need the perpendicular component:
V⊥=Vsinθ
Using sinθ=√1−cos2θ=√1−0.92=√0.19≈0.43589:
V⊥=2m/s⋅√0.19≈2⋅0.43589≈0.87178m/s
Step 4: Calculate the kinetic energy
The kinetic energy K of the pendulum just after the lift-off is given by:
K=12mV2⊥
Substituting the values:
K=12⋅0.1kg⋅(0.87178m/s)2
Calculating (0.87178)2:
(0.87178)2≈0.7602
Now substituting back into the kinetic energy formula:
K≈12⋅0.1⋅0.7602≈0.03801J
Thus, the value of K is approximately 0.038J.
Final Answer
The value of K is 0.038J.
---
The impulse P given to the bob is 0.2kg m/s. The mass m of the bob is 0.1kg. The velocity V of the bob after the impulse can be calculated using the formula:
When the bob lifts off, it forms an angle θ with the vertical. The height h from which the bob is suspended is 0.9m and the length of the string l is 1.0m.
The velocity V can be resolved into two components:
- Along the string: Vcosθ
- Perpendicular to the string: Vsinθ
The kinetic energy K of the pendulum just after the lift-off is given by:
The value of K is 0.038J.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
Aangular momentum is conserved.Bangular momentum changes in magnitude but not is direction.Cangular momentum changes in direction but not in magnitude.Dangular momentum changes both in direction and magnitude.A simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
AmL√2gLBmL√gLCmL√3gLDnone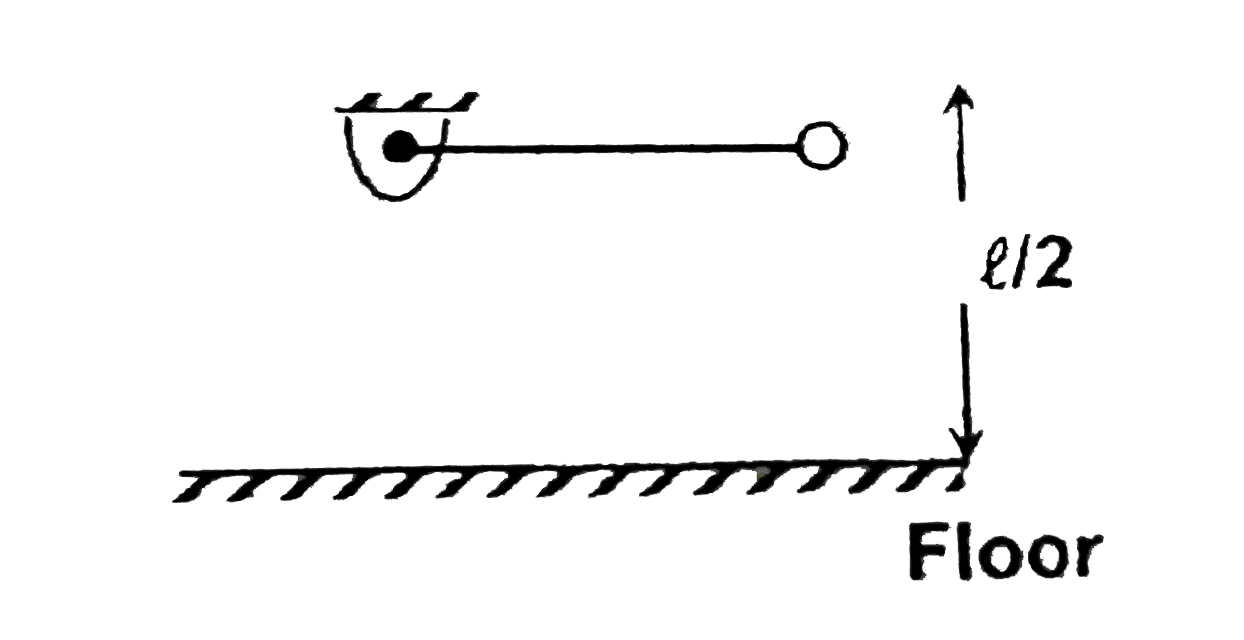
A bob of mass m connected to the end of an inextensible string of length l, is released from position shown in figure. If impacts of bob with smooth floors is perfectly inelastic. Choose the correct options (s)AThe maximum height reached by the bob during subsequency motion is l32BMaximum height reached by the bob during subsequency motion is zero.CEnergy loss from the time duration bob is released to the time it reaches at its maximum height during subsequent motion is 3mgl8DEnergy loss from the time duration bob is released to the time it reaches to the time it reaches at its maximum height during subsequency motion is 15mgl32
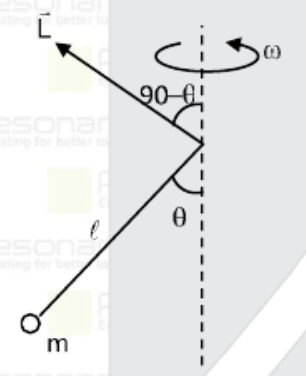
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionA bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View Solution
A simple pendulum consists of a bob of mass m and a light string of length l as shown in the fig. another identical ball moving with the small velocity v0 collides with the pendulum's bob and sticks to it. For this new pendulum of mass 2 m, mark out the correct statements (s).
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View Solution
