A particle of mass m oscillates with simple harmonic motion between two points x1 and x2 the equilibrium position being O its potential energy is plotted on the graph which of the following curve represents the phenomenon?

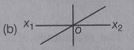
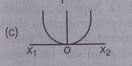
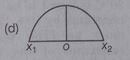
The correct Answer is:C
Similar Questions
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
View SolutionA particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
View Solution
Knowledge Check
A particle of mass m oscillates with simple harmonic motion between points x1 and x2 the equilibrium position being O its potential energy in plotted it will be as given bellow in the graph
A B
B C
C D
D
A particle of mass m oscillates with simple harmonic motion between points x1 and x2, the equilibrium position being O. Its potential energy is plotted. It will be as given below in the graph
A B
B C
C D
D
The potential energy of a particle, executing a simple harmonic motion, at a dis"tan"ce x from the equilibrium position is proportional to
A√xBxCx2Dx3
A particle is vibrating in a simple harmonic motion with an amplitude of 4 cm . At what displacement from the equilibrium position, is its energy half potential and half kinetic
View SolutionA particle oscillates simple harmonic motion with a period of 16s. Two second after crossing the equilibrium position its velocity becomes 1m/s. The amplitude is
View SolutionA particle executes simple harmonic motion of ampliltude A. At what distance from the mean position is its kinetic energy equal to its potential energy?
View SolutionA particle is vibrating in a simple harmonic motion with an amplitude of 4 cm . At what displacement from the equilibrium position, is its energy half potential and half kinetic
View SolutionA particle oscillates simple harmonic motion with a period of 16s. Two second after crossing the equilibrium position its velocity becomes 1m/s. The amplitude is
View Solution
