In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
Step by step video & image solution for In Figure the line segment XY is parallel to side AC of DeltaA B Cand it divides the triangle into two parts of equal areas. Find the ratio (A X)/(A B). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
8 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Very Short Answer type Questions )
17 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Very Short Answer Type Questions )
13 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
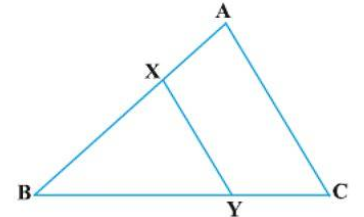
View SolutionIn the given figure, line the segment XY is parallel to side AC of ΔABC and it divides the triangles into two parts of equal area. Prove that AX:AB=(2−√2):2
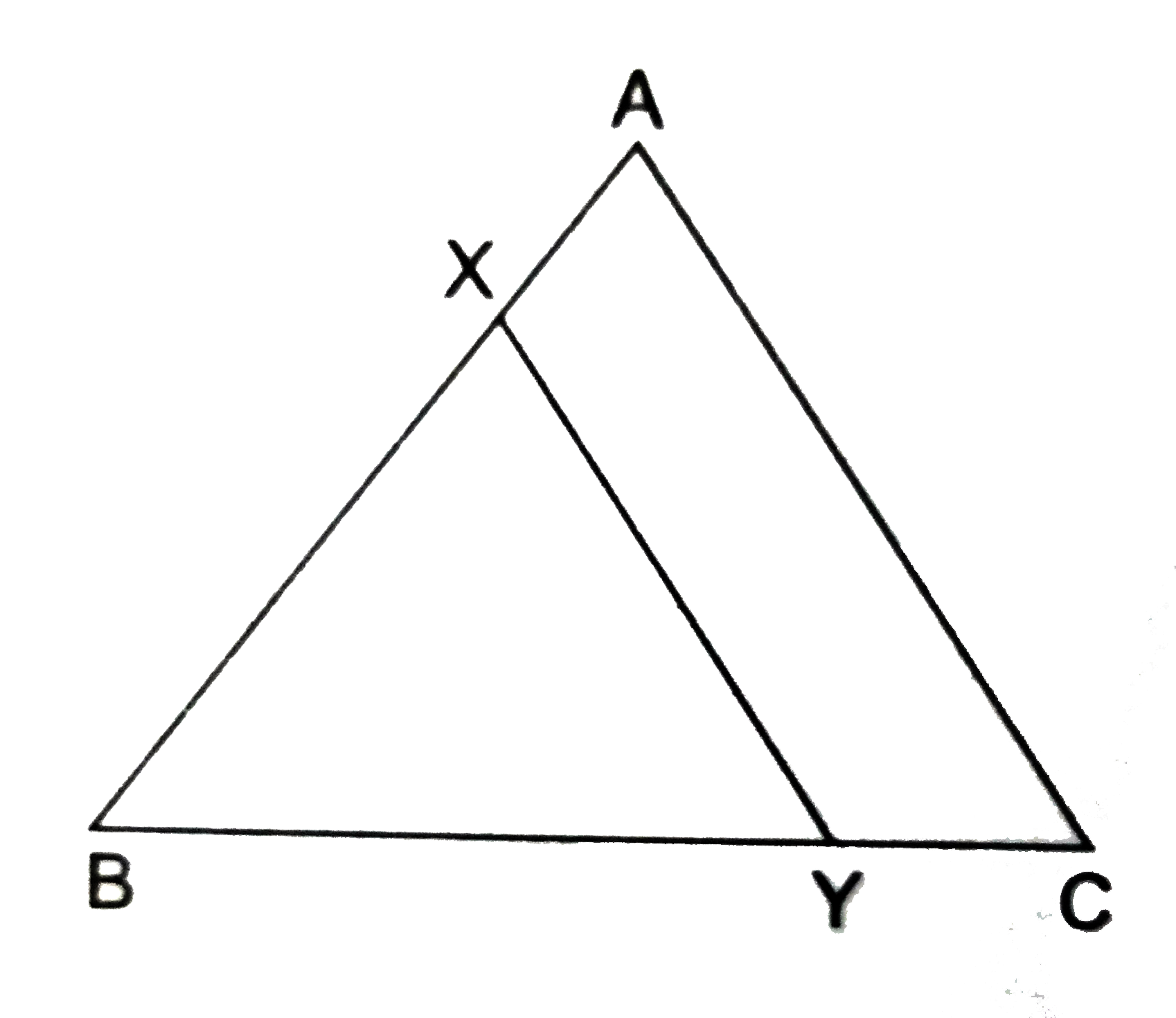
View Solution
Knowledge Check
In Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
A√2+1+√2B2−√2:2C1:√2D1:1In ΔABC, XY is parallel to BC and it divides the triangle into two equal areas (X lies on AB and Y lies on AC) then BX:AB equals
A√2:√2−1B1:1C2:1D√2−1:√2In the figure given below, XY parallel to AC. If XY divides the triangle into equal Parts, then value of AX/ AB is equal to
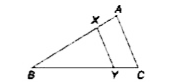 A12B1√2C√2+1√2D√2−1√2
A12B1√2C√2+1√2D√2−1√2
In the given figure, the line segment XY is Parallel to AC of ΔABC and it divides the triangle into two parts of equal areas. Prove that AXAB=√2−1√2
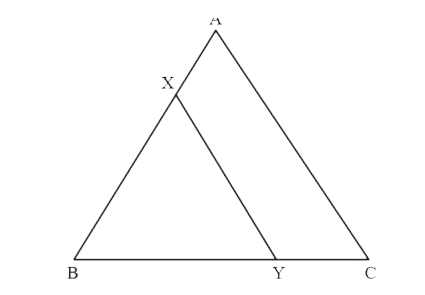
View SolutionIn the given figure, XY∣∣ACandXY divides ΔABC into two regions, equal in area. Find the value of AXAB
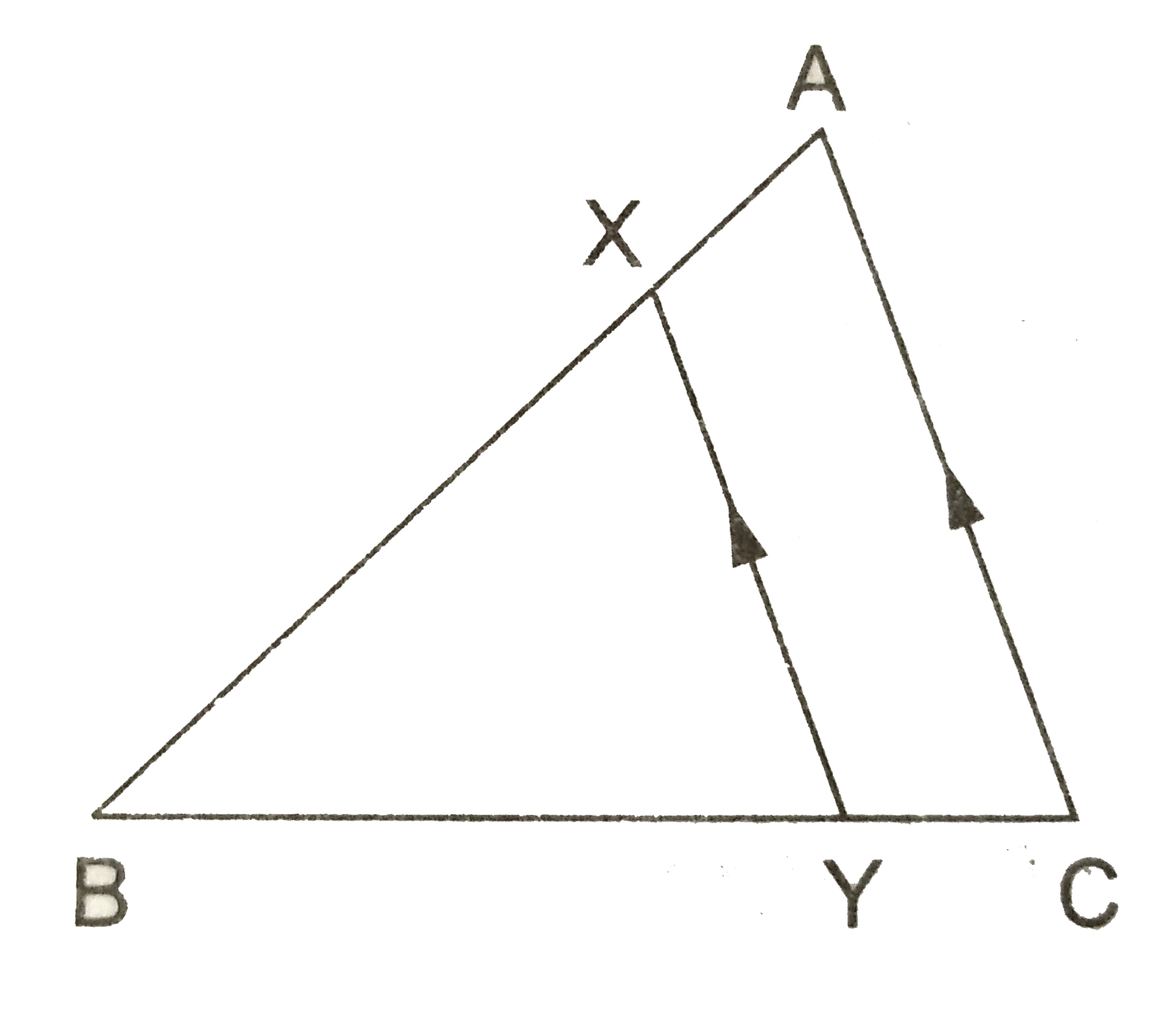
View SolutionIn ΔABC seg MN∣∣ side AC. Seg MN divides ΔABC into two parts equal in area. Determine MBAB.
View SolutionIn ABC , PQ is a line segment intersecting AB at P and AC at Q such that PQBC and PQ divides ABC into two parts equal in area. Find BPAB .
View SolutionIn △ABC, F and E are the points on sides AB and AC respectively, such that FE || BC and FE divides the triangle in two parts of equal area. If AD⊥BC and AD intersect FE at G, then GD: AG = ?
△ABC में F और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि FE || BC है तथा FE त्रिभुज को बराबर क्षेत्रफल वाले दो भागों में विभाजित करती है | यदि AD⊥BC है और AD, FE को G पर काटती है, तो GD: AG = ?
View Solution
