Assertion (A): Two resistance having value R each. Their equivalent resistance is R2.
Reason (R): Given Resistance are connected in parallel.
Both A and R are true and R is the correct explanation of A.
Both A and R are true but R is NOT the correct explanation of A
A is true but R is false.
A is false and R is true.
The correct Answer is:A
To solve the assertion and reason question, we need to analyze both the assertion (A) and the reason (R) provided.
1. Understanding the Assertion (A):
- The assertion states that "Two resistances having value R each have an equivalent resistance of R/2."
- This implies that the two resistances are connected in such a way that their combined effect on the circuit results in a total resistance of R/2.
2. Understanding the Reason (R):
- The reason states that "The given resistances are connected in parallel."
- In electrical circuits, when resistors are connected in parallel, the total or equivalent resistance can be calculated using the formula:
1Req=1R1+1R2
- For two resistors of equal value R, this becomes:
1Req=1R+1R=2R
- Therefore, the equivalent resistance Req is:
Req=R2
3. Conclusion:
- Since the calculation confirms that the equivalent resistance of two resistors R connected in parallel is indeed R/2, we can conclude that both the assertion and the reason are true.
- Furthermore, the reason correctly explains why the assertion is true.
Final Answer:
- Both Assertion (A) and Reason (R) are true, and R is the correct explanation of A.
- The assertion states that "Two resistances having value R each have an equivalent resistance of R/2."
- This implies that the two resistances are connected in such a way that their combined effect on the circuit results in a total resistance of R/2.
- The reason states that "The given resistances are connected in parallel."
- In electrical circuits, when resistors are connected in parallel, the total or equivalent resistance can be calculated using the formula:
1Req=1R1+1R2
- For two resistors of equal value R, this becomes:
1Req=1R+1R=2R
- Therefore, the equivalent resistance Req is:
Req=R2
- Since the calculation confirms that the equivalent resistance of two resistors R connected in parallel is indeed R/2, we can conclude that both the assertion and the reason are true.
- Furthermore, the reason correctly explains why the assertion is true.
- Both Assertion (A) and Reason (R) are true, and R is the correct explanation of A.
Similar Questions
In the given circuit all resistances are of value R ohm each. The equivalent resistance between A and Bis :
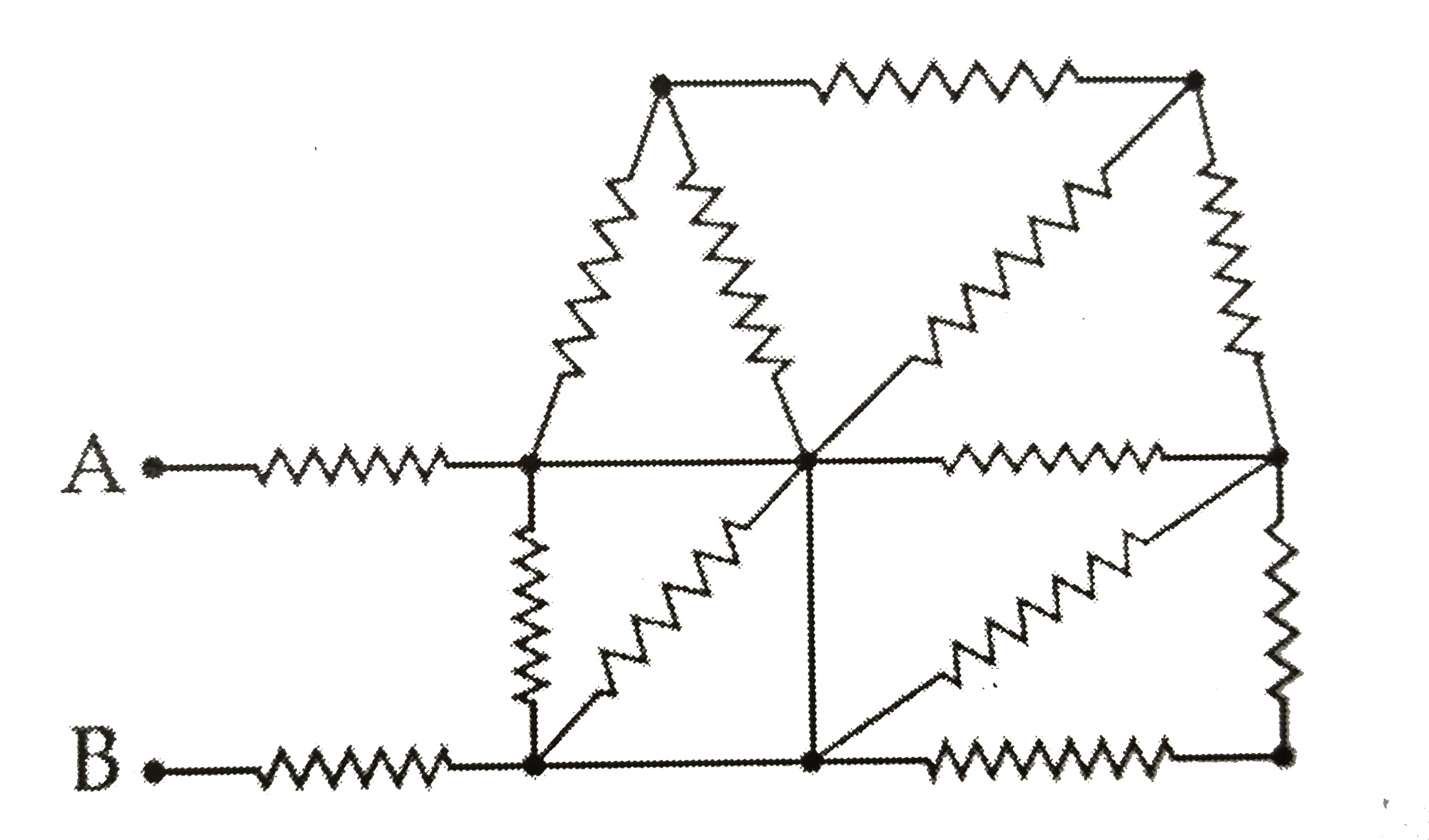 View Solution
View SolutionTwo resistance R1andR2 when connected in series produce equivalent resistance equal to x. and when the same two resistance are connected in parallel then equivalent resistance becomes y. Calculate the product of magnitudes of R1andR2 in terms of x and y.
View Solution
Knowledge Check
- Question 1 - Select One
The effective resistance of three equal resistances, each of resistance r, connected in parallel, is
A3/rBr/3C3rDr3 - Question 2 - Select One
Assertion (A): Resistances connected in parallel has higher equivalent resistance.
Reason (R): RP=R1+R2+….+RnABoth (A) and (R) are true and (R) is the correct explanation of (A).BBoth (A) and (R) are true but (R) is not the correct explanation of (A).C(A) is true but (R) is false.D(A) is false and (R) is also false. - Question 3 - Select One
Assertion (A): Resistances connected in parallel has higher equivalent resistance.
Reason (R): RP=R1+R2+…+RnABoth (A) and (R) are true and (R) is the correct explanation of (A).BBoth (A) and (R) are true but (R) is not the correct explanation of (A).C(A) is true but (R) is false.D(A) is false but (R) is also false.
Assertion (A): In series grouping of resistances the equivalent resistance is greater than even the biggest resistance joined in series.
Reason (R ): In series arrangement the equivalent resistance Rs is given as per the relation 1R=1R1+1R2+1R3+......View SolutionResistance of each resistor is R. Then the equivalent resistance across A and B is
 View Solution
View SolutionEquivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
View SolutionThe resultant resistance value of n resistance each of r ohms and connected is series is X. When those n , resistance are connected in parallel , the resultant values is .
View SolutionEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
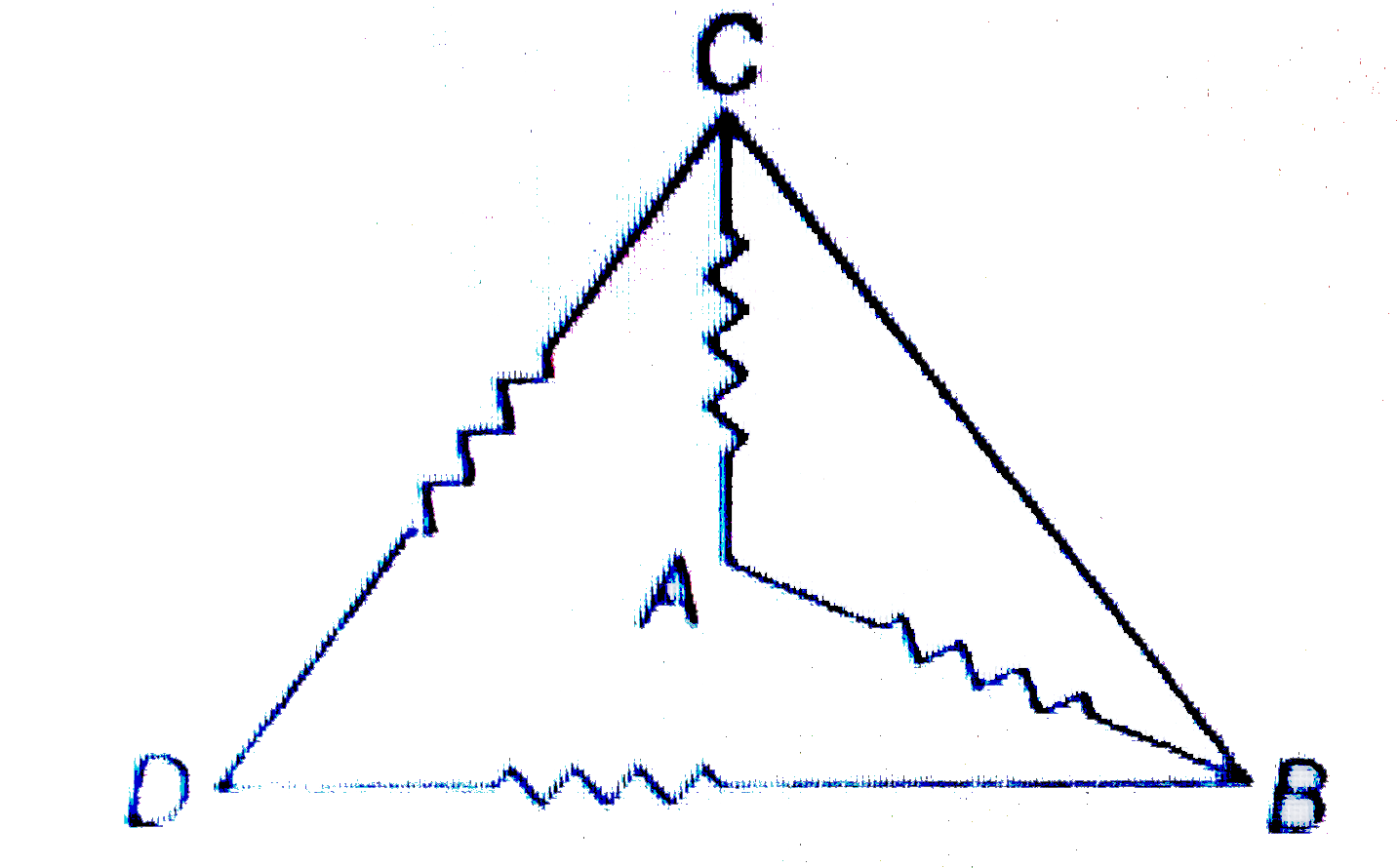 View Solution
View Solution

