A block of mass m and relative density y(<1) si attached to an ideal spring of constant K. The system is initially at rest and at equilibrium. If the container acceleration upwards with a0, find the increase in the elongation of the spring in equilibrium.
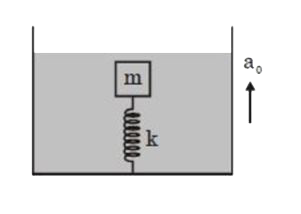
ma0γK
ma0K(1−γ)
ma0K(1γ−1)
ma0K(γ−1)
The correct Answer is:C
Initially
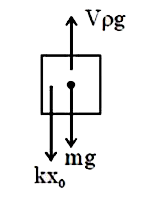
⇒Vpg=kx0+mg…(i)
Finally
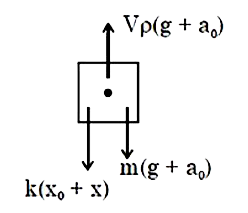
⇒Vρ(g+a0)=k(x0+x)+m(g+a0)…(ii)
(ii)−(i)
Vρa0=kx+ma0
x=Vpa0−mak
x=ma0k(Vρm−1)
x=ma0k(VρVρm−1)
x=ma0k(1γ−1)
Topper's Solved these Questions
- NTA TPC JEE MAIN TEST 47BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 47EXERCISE - PHYSICS (SUBJECTIVE NUMERICAL)
10 Videos
- NTA TPC JEE MAIN TEST 46BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 46EXERCISE - PHYSICS
30 Videos
- NTA TPC JEE MAIN TEST 48BOOK - NTA MOCK TESTSCHAPTER - NTA TPC JEE MAIN TEST 48EXERCISE - PHYSICS
29 Videos
Similar Questions
A block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
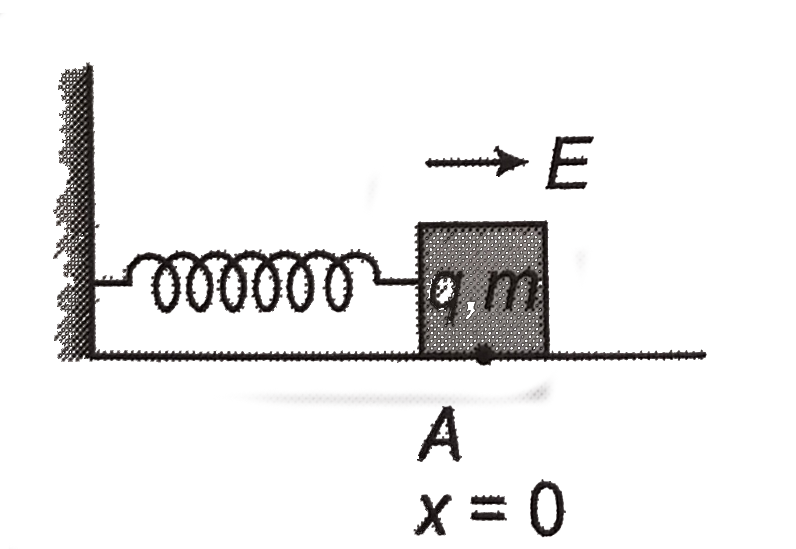
View SolutionA block of mass m can slide along a frictionless inclined plane, is attached to a ideal spring of spring constant as shown in the figure. Find the period of its oscillation. (Frame of reference attached to the wedge is at rest)
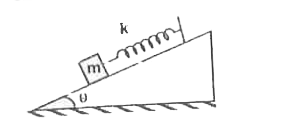
View Solution
Knowledge Check
A block is attached with an ideal spring and string, and is in equilibrkum as shown in Figure. The acceleration of the block just after breaking the string is a1 and just after breaking the spring is a2. Then
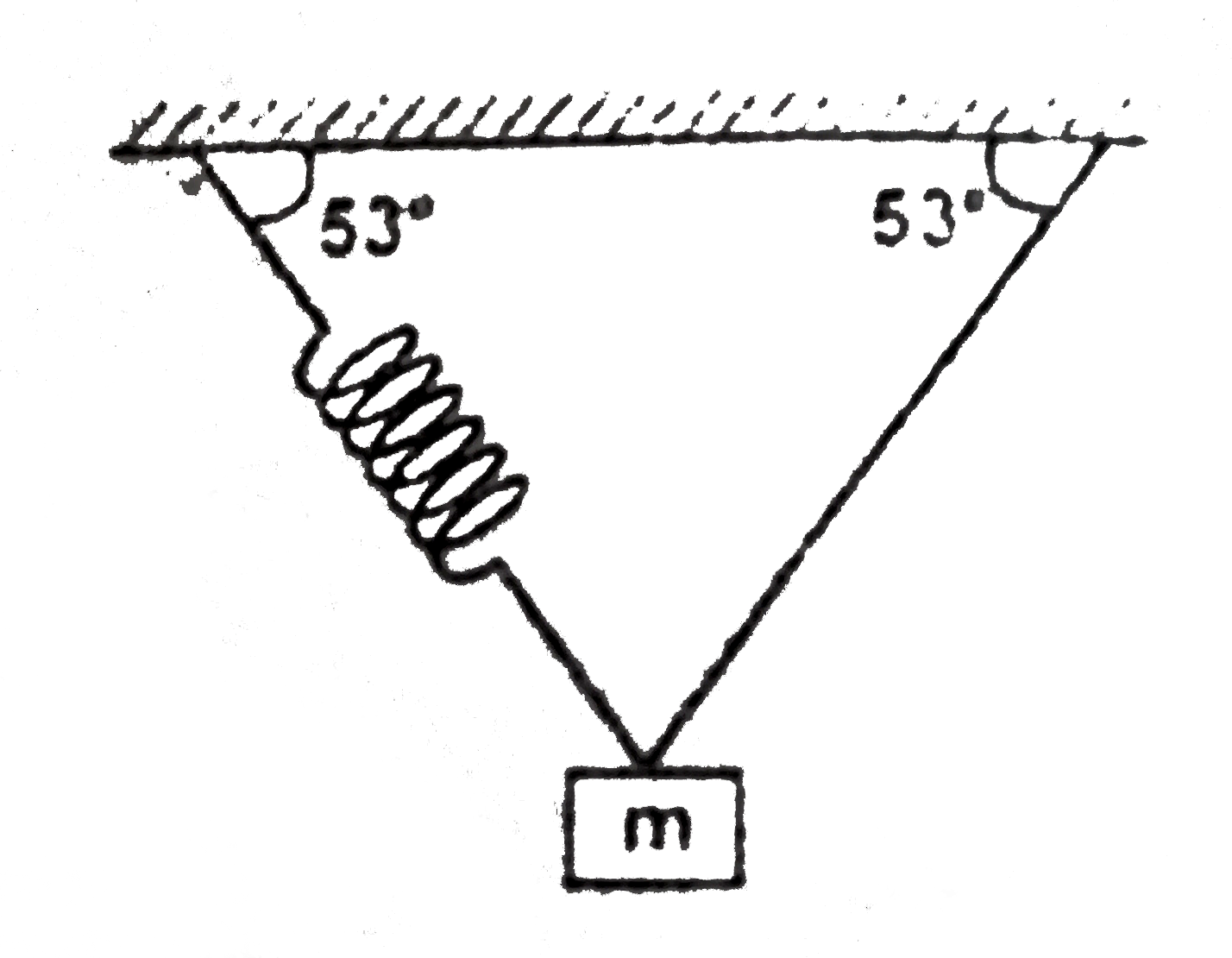 Aa1=5g8Ba2−3g5Ca1=g2Da2=g
Aa1=5g8Ba2−3g5Ca1=g2Da2=gA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
 AmakB12makC2makD124mak
AmakB12makC2makD124mak
A block of mass 5kg having charge q is attached to a spring of constant K=104N/m. A charge −q is placed below the block at separation 0.5m. If the maximum elongation of spring is 0.5m. If the maximum elongation of spring is 0.1m, find q. Assume the initial elongation of spring is zero.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
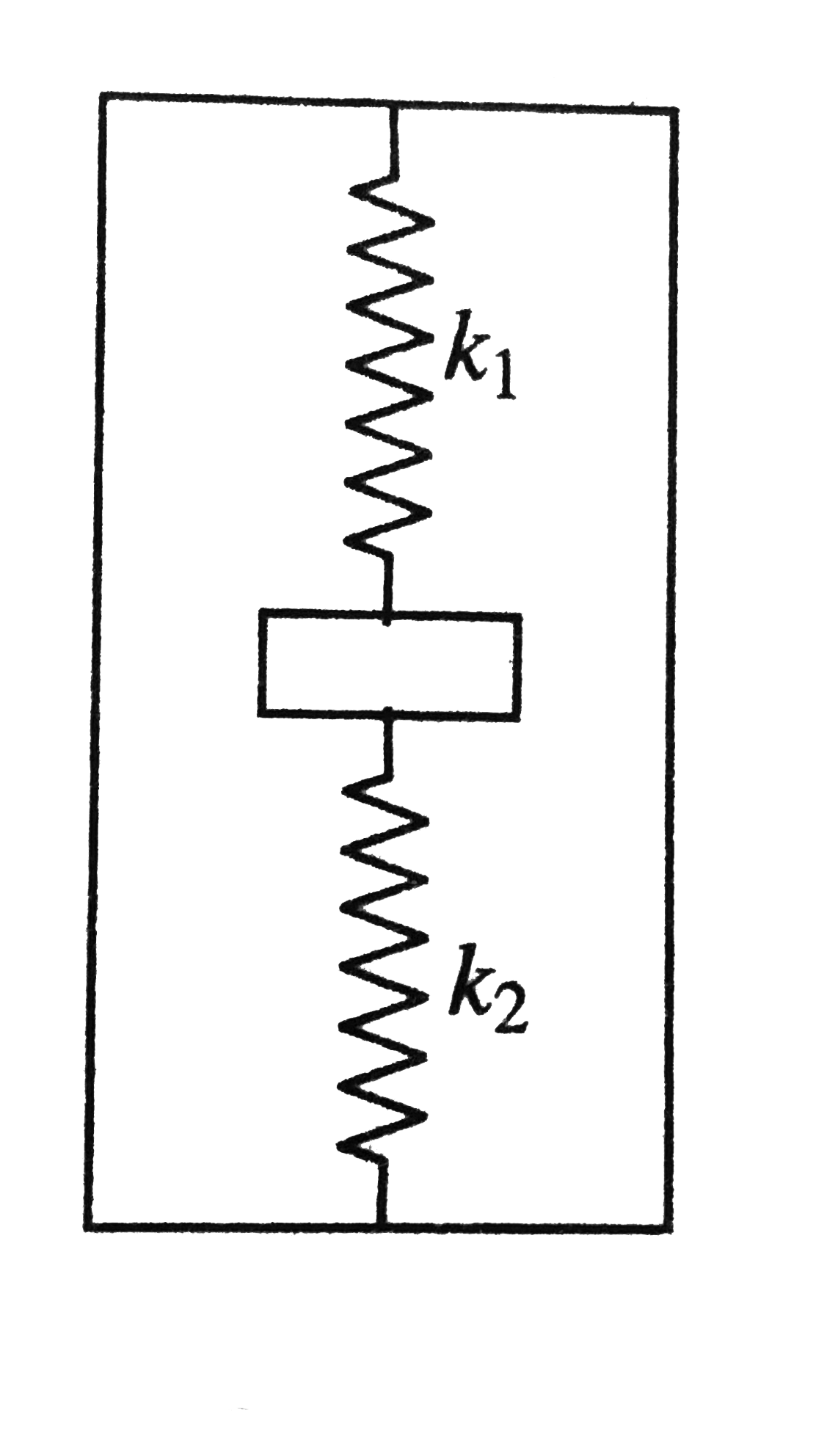
View SolutionA pulley with two blocks system is attached to the ceiling of a lift upward with an acceleration a0 . Find the deformation in the spring.
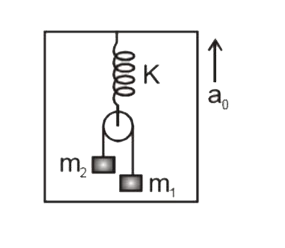
View SolutionA bullted of mass m embeds itself in a block of mass M resting on a smooth horizontal surface, attached to a spring of force constant k. If the initial sped of the bullet is v0 along horizontal, find (a) the maximum compression of the spring and (b) the time forthe bullet - block system to come to rest.
View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View Solution
