Question

A solid cylinder has diameter D and length L. Find its moment of inertia about an axis perpendicular to its length and passing through the centre of gravity.

Options

A. `M[D^(2)/4 + L^(2)/12]`
B. `M[D^(2)/16 + L^(2)!2]`
C. `M[D^(2)/8 + L^(2)/12]`
D. `M[D^(2)/4 + L^(2)/6]`

Answer

B

Explanation

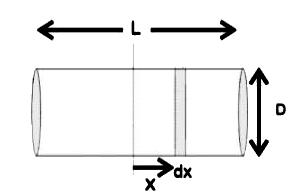
Let us consider an element of the cylinder, which is a disc of thickness dx at a distance x from the center. Density of cylinder, `rho = ("Mass")/("Volume")`
`rArr rho = M/(pi(D/2)^(2)L)`
Mass of the element, `dm = rhodV`
`rArr dm = rho((piD^(2))/4 dx)`
`rArr dm = M/L dx`
Moment of inertia of a disc of mass m and radius r about an axis passing through its center and lying in its plane is `I_("Disc") = (mr^(2))/4`
Parallel axis theorem is given by: `I = I_(cm) + md^(2)`
Using these concepts we can say that moment of inertia of the given element of the cylinder about an axis passing through the center of the cylinder is:
`dI = ((dm)R^(2))/4 + (dm)x^(2)`
`rArr dI = ((dm)D^(2))/16 + (dm)x^(2)`
`rArr dI = (MD^(2))/(16L) dx + M/L x^(2) dx`
Moment of inertia of the cylinder is, `I = int I`
`rArr I = int_(x = - L/2)^(x = L/2) (MD^(2))/(16 L) dx + int_(x = -L/2)^(x = L/2) M/L x^(2) dx`
`rArr I = (MD^(2))/16 x |_(L/2)^(L/2) + M/(3L) x^(3) |_(-L/2)^(L/2)`
`rArr I = (MD^(2))/16 + (ML^(2))/12`