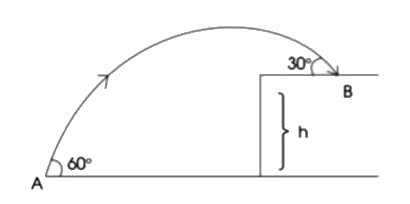
What is the speed of projection of a particle which strikes the roof of building at B at an angle of 30° with the horizontal, after being projected from point A towards a building of height h as shown at an angle of 60° with horizontal ?
√gh
√2gh
√3gh
2√gh
The correct Answer is:C
Let u be the speed of projection and v be the speed at B
ucos60∘=vcos30∘
⇒v=u√3 .............. (i)
Applying law of conversation of energy.
12mv2−12μ2=−mgh...... (ii)
Using equation (i) in equation (ii), we have u=√3gh
Topper's Solved these Questions
Similar Questions
Two bodies are projected from the same point of a plane with the same speeds and at different angles of projection so that they both strike the same point on a plane which is inclined at an angle of 30∘ with the horizontal. If first body was projected at an angle of 45∘ with the horizontal, then find out the ratio of their times of flight.
View SolutionIf a particle of mass m is thrown with speed at an angle 60° with horizontal, then angular momentum of particle at highest point about point of projection is
View Solution
Knowledge Check
A particle at a height h from the ground is projected with an angle 30∘ from the horizontal, it strikes the ground making angle 45∘ with horizontal. It is again projected from the same point with the same speed but with an angle of 60∘ with horizontal. Find the angle it makes with the horizontal when it strikes the ground
Atan−1(4)Btan−1(5)Ctan−1(√5)Dtan−1(√3)a particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dma particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
A21dmB2.1dmC30dmD6dm
A particle is projected from a point on the ground surface at different angles keeping the speed of projection as constant range obtained is plotted as function of the angle of projection with the horizontal 'O'. Find the range obtained if particle is projected at angle 30° with the horizontal : 2 g 10 m/s 250m R
View SolutionA ball is projected at an angle 60∘ with the horizontal with speed 30 m/s. What will be the speed of the ball when it makes an angle 45∘ with the horizontal ?
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
View SolutionA particle is projected from the ground at an angle of 60∘ with horizontal at speed u=20m/s. The radius of curvature of the path of the particle, when its velocity. makes an angle of 30∘ with horizontal is :
(g=10m/s2
View Solution
