A uniform rod AB of mass m is suspended in equilibrium from two similar springs as shown. If spring 2 breaks, then the angular acceleration of the bar at that instant will be
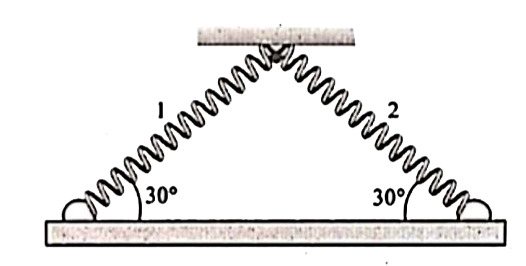
2gl
2g3l
3gl
g3l
The correct Answer is:C
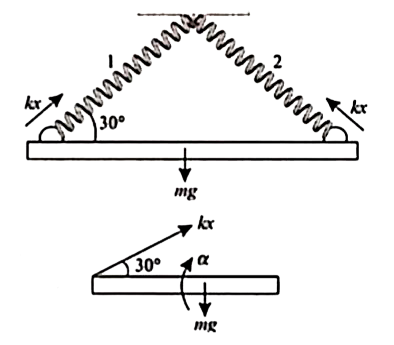
m equilibrium
2kxsin30∘=mg
kx = mg...(i)
When spring is snapped
Equation of rotation motion about COM.
kx.sin30∘12=Iα
=ml212α⇒α=3g1
Topper's Solved these Questions
Similar Questions
Knowledge Check
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmA block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .
 A(mg)24kB(mg)22kC(mg)28kD(mg)2k.
A(mg)24kB(mg)22kC(mg)28kD(mg)2k.
A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1 and k2. The time period of the suspended mass will be
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1andk2. The time period of the suspended mass will be
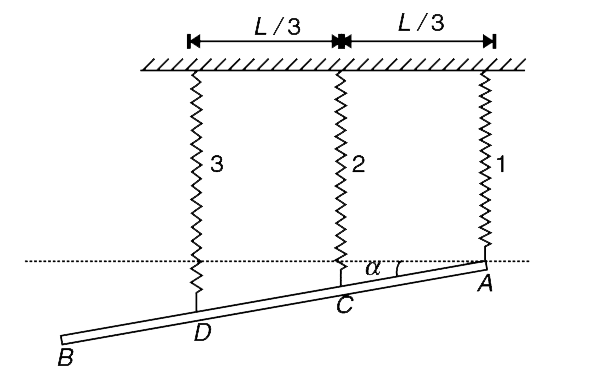
View SolutionA uniform rod AB has mass M and length L. It is in equilibrium supported in vertical plane by three identical springs as shown in figure. The springs are connected at A, C and D such that AC=CD=L3. Assume that the springs are very stiff and the angle a made by the rod with the horizontal in equilibrium position is very small. (All springs are nearly vertical). Calculate the tension in the three springs.
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
View Solution
