Consider two particles of equal mass m. If one particle is stationary while the other collides with this particle obliquely with velocity v. Now, what is the angle between the velocity vectors of the two particles after the collision?

A

$45^{\circ}$

B

$30^{\circ}$

C

$90^{\circ}$

D

none of these

Text Solution

Verified by Experts

The correct Answer is:C

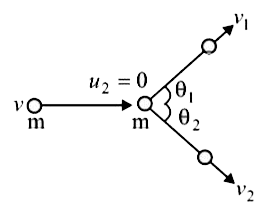
Given that mass of each particle = m
initial velocity of one moving particle = v
initial velocity of other particle = 0 (because it is stationary)
Let after collision,
One particle moves with velocity $v_{1}$ with angle $θ_{1}$ w.r.t. -axis, and other particle moves with velocity $v_{2}$ with angel $θ_{2}$ w.r.t. x axis.
Now, by momentum conservation in x-direction (initial momentum) along x-axis.
= (final momentum) along y-axis ${(p_{i})}_{x - axis} = {(p_{f})}_{x - axis}$
$\Rightarrow m v + m (0) = m v_{1} {cos θ}_{1} + m v_{2} {cos θ}_{2}$
$\Rightarrow v = v_{1} {cos θ}_{1} + v_{2} {cos θ}_{2} ... (1)$
Now, by momentum conservation in y-direction
${(p_{i})}_{y-axis} = {(p_{f})}_{y-axis}$
$\Rightarrow m (0) + m (0) = m v_{1} sin$
$θ_{1} - m v_{2} {sin θ}_{2}$
$\Rightarrow 0 = v_{1} {sin θ}_{1} - v_{2} {sin θ}_{2} ... (2)$
and by law of conservation of kinetic energy
${(Kinetic energy)}_{before collision} = {(Kinetic energy)}_{after collision}$
$\Rightarrow \frac{1}{2} m v^{2} + \frac{1}{2} m {(0)}^{2} = \frac{1}{2} m v_{1}^{2} + \frac{1}{2} m v_{2}$
$\Rightarrow v^{2} = v_{1}^{2} + v_{2}^{2} ... (3)$
Addition of square of eq. (1) and eq. (2)
$\Rightarrow v^{2} + 0^{2} = {(v_{1} {cos θ}_{1} + v_{2} {cos θ}_{2})}_{1}^{2} + {(v_{1} {sin θ}_{1} - v_{2} {sin θ}_{2})}_{1}^{2}$
$\Rightarrow v^{2} = v_{1}^{2} {cos θ}_{1}^{2} + v_{2}^{2} {cos θ}_{2}^{2} + 2 v_{1} v_{2} {cos θ}_{1} {cos θ}_{2} + v_{1}^{2} {sin θ}_{1}^{2} + v_{2}^{2} {sin θ}_{2}^{2} - 2 v_{1} v_{2} {sin θ}_{1} {sin θ}_{2}$
$\Rightarrow v^{2} = v_{1}^{2} ({cos θ}_{1}^{2} + {sin θ}_{2}^{2}) + v_{2}^{2} ({cos θ}_{2}^{2} + {sin θ}_{2}^{2})$
$2 v_{1} v_{2} ({cos θ}_{1} {cos θ}_{2} - {sin θ}_{2} {sin θ}_{2})$
$\Rightarrow v^{2} = v_{1}^{2} + v_{2}^{2} + 2 v_{1} v_{2}$
$({cos θ}_{1} {cos θ}_{2} - {sin θ}_{1} {sin θ}_{2})$
Using eq.(3)
$\Rightarrow v_{1}^{2} + v_{2}^{2} = v_{1}^{2} + v_{2}^{2} + 2 v_{1} v_{2} ({cos θ}_{1} {cos θ}_{2} - {sin θ}_{1} {sin θ}_{2})$
$\Rightarrow 2 v_{1} v_{2} cos (θ_{1} + θ_{2}) = 0$
$\Rightarrow cos (θ_{1} + θ_{2}) = 0$
$\Rightarrow θ_{1} + θ_{2} = {cos}^{- 1} (0) = 90$
So, angle between the velocity vectors of the two particles after the collision is $90^{\circ}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

The velocity vector of a stationary particle is __________
Azero vector
Bvector with magnitude of velocity vector
Cscalar
Dscalar with magnitude of velocity vector

NTA MOCK TESTS-NTA TPC JEE MAIN TEST 63-PHYSICS

Home
Ask Doubt
Profile