A soap bubble has surface tension 'T' and its radius 'p'. The mean square velocity of air molecules insidev1 and outside v2. Given that v1−v2=(aTrρ), where 'ρ' and 'a' is a constant, then the value of ’a’= ____
The correct Answer is:A, B
For soap bubble the excess pressure inside is, ΔP=4Tr
From kinetic theory of gases,
P=13ρc2
∴(c2)in=−(c2)out=3ρ(Pin−Powt)
=3ρΔP
=3ρ(4Tr)
∴(aTrρ)−12Trp
∴a=12
Topper's Solved these Questions
Similar Questions
Knowledge Check
Excess pressure inside a soap bubble of radius r and surface tension T is
A2TrB4TrCT2rDT4rA bubble having surface tension T and radius R is formed on a ring of radius b(b<<R). Air is blown inside the tube with velocity v as shown. The air molecule collides perpendicularly with the wall of the bubble and stops. Calculate the radius at which the bubble separates from the ring.
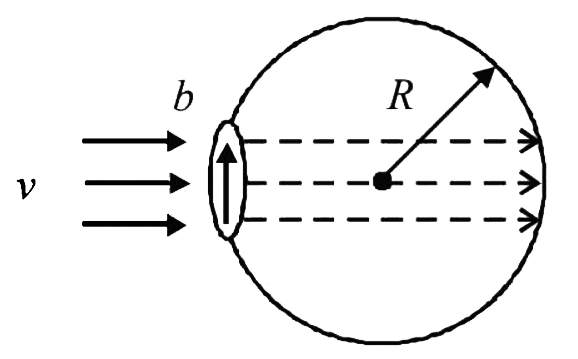 A1. 2Tρv2B2. 2TρvC3. 4Tρv2D4. 4Tρv
A1. 2Tρv2B2. 2TρvC3. 4Tρv2D4. 4TρvSurface charge density of soap bubble of radius r and surface tension T is σ.If P is excess pressure the value of σ is
Aε0[4Tr−P]32B[2ε0(4Tr−P)]12C4TrD[4ε0(2Tr−P)]12
If v1 and v2 denote the sound velocity'and root mean square velocity of molecules of an ideal gas then select the correct option (γ = adiabatic constant)
View SolutionIf v1 and v2 denote the sound velocity'and root mean square velocity of molecules of an ideal gas then select the correct option (γ = adiabatic constant)
View SolutionA bubble having surface tension T and radius R is formed on a ring of radius b (b<>R) . Air is blown inside the tube held in front of the ring , with velocity υ as shown in fig. The air molecules collides perpendicularly with the wall of the bubble and stops. Calculate the radius R at which the bubble and stops. Calculate the radius R at which the bubble separates from the ring.
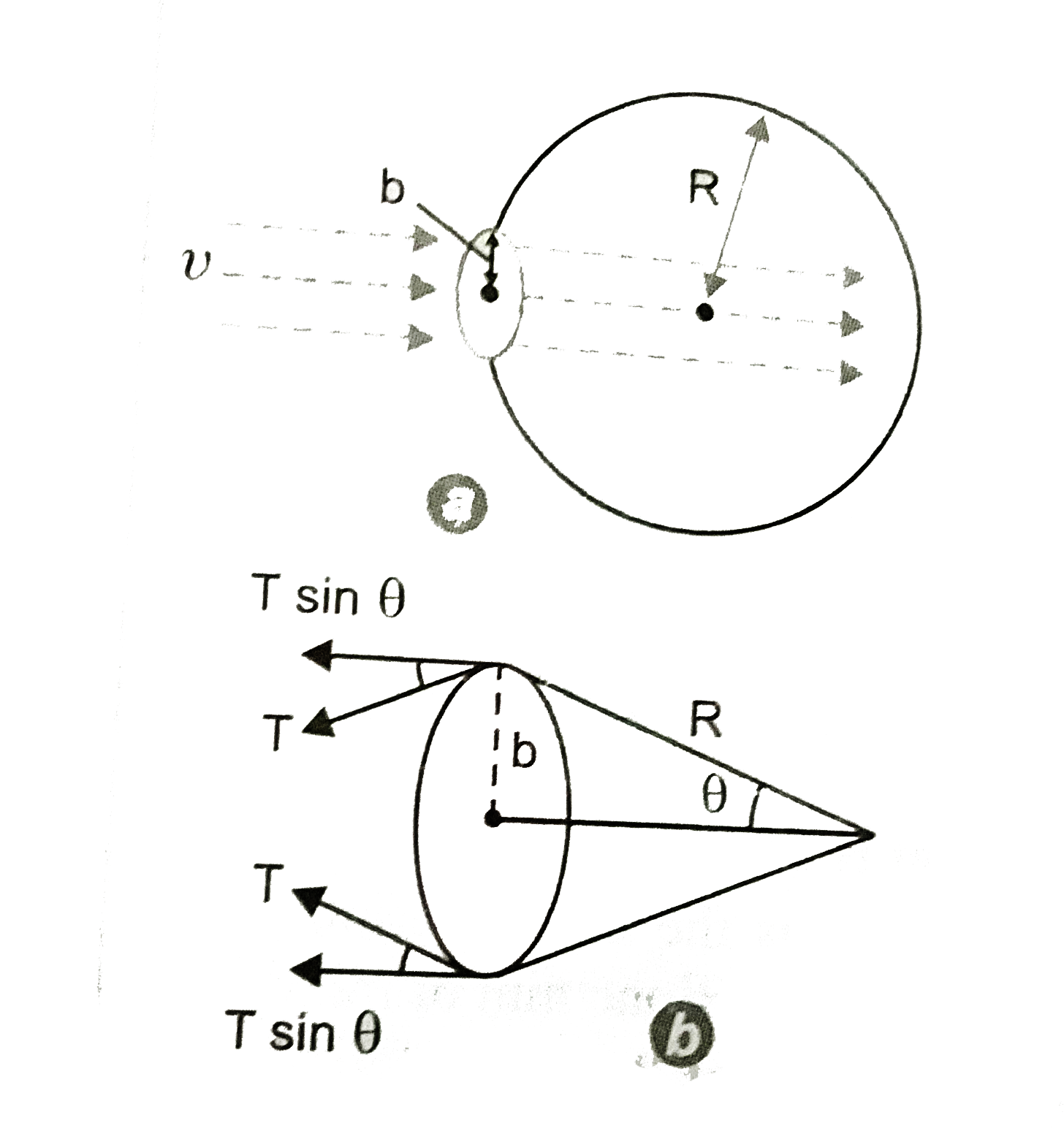
View SolutionA bubble having surface tension T and radius R is formed on a ring of radius b (b<>R) . Air is blown inside the tube held in front of the ring , with velocity υ as shown in fig. The air molecules collides perpendicularly with the wall of the bubble and stops. Calculate the radius R at which the bubble and stops. Calculate the radius R at which the bubble separates from the ring.

View SolutionThe escape velocities of the two planets, of densities ρ1 and ρ2 and having same radius, are v1 and v2 respectively. Then
View Solution
