Question

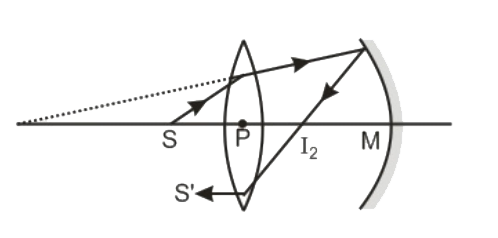
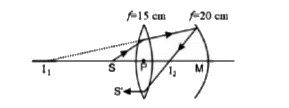
A converging lens of focal length 15 cm and a converging mirror of focal length 20 cm are placed with their principal axes coinciding. A point source S is placed on the principal axis at a distance of 12 cm from the lens, as shown in figure. It is found that the final beam comes out parallel to the principal axis. Let the separation between the mirror and the lens be $10\times k$. Find k.

Answer

4

Explanation

Let us first locate the image of S formed by the lens L. Let.s name this first image be `I_(1)` .
Here, u = -12 cm and f = 15 cm
We have
`(1)/(v ) - (1)/( u) = (1)/(f )`
or `(1)/( v ) = (1)/(f ) + (1)/(u)`
`(1)/(v) = (1)/(15) - (1)/(12)`
or `v = - 60` cm .

`SP =12 cm , PI_(2) =15 cm , MI_(2)=x cm`
The negative sign shows that the image is formed to the left of the lens as suggested In the figure. The image Ii acts as a source for the mirror. The mirror forms an Image 12 of the source 11. This Image h then acts as a source for the lens and the final beam comes out parallel to the principal axis. Clearly, h must be at the focus of the lens. We have,
`I_(1) I_(2) = I_(1) P + PI_(2) `=60 cm + 15 cm = 75 cm
Suppose the distance of the mirror from `I_(2)` is x cm. For reflection from the mirror,
`u = MI_(1) = `- (75 +x) cm v = -x
cm and f = - 20 cm
Using `(1)/(v ) + (1)/(u) = (1)/(f )`
`(1)/(x ) - (1)/(75 +x) = (1)/(20)`
or `(75 +2x)/((75+x)x)= (1)/(20)`
or `x^(2) + 35 x ` - 1500 =0
or `x = (-35 pm sqrt(35xx 35 +4 xx 1500))/(2 )`
This gives x = 25 or - 60
As the negative sign has no physical meaning, only the positive sign should be taken. Taking x = 25, the separation between the lens and the mirror is, (15 + 25) cm = 40 cm.
Hence K =4