Consider a horizontal surface moving vertically upward with velocity $2 m s^{- 1}$ . A small ball of mass 2 kg is moving with velocity $(2 ˆ i - 2 ˆ j) m s^{- 2}$ If the coefficient of restitution and coefficient of friction are $\frac{1}{2} and \frac{1}{3}$ respectively, find the horizontal velocity $(in m s^{- 1})$ of the ball after the collision.

Video Solution

Text Solution

Verified by Experts

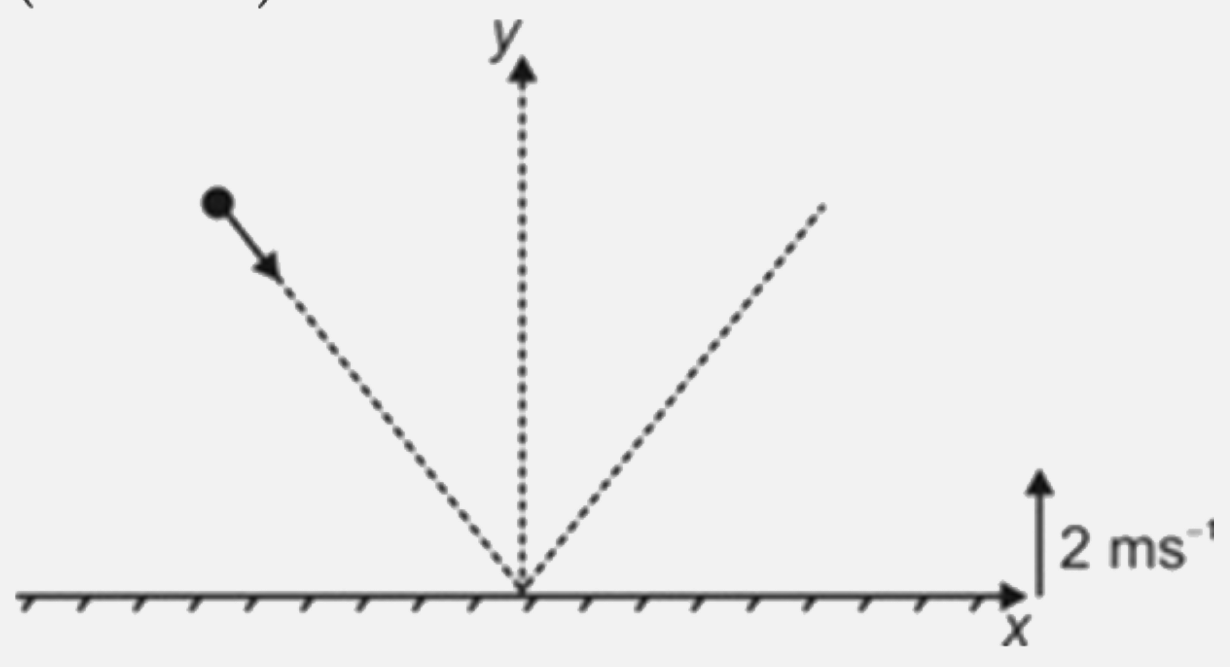
The correct Answer is:0

Updated on:21/07/2023

A body of mass 1000 kg is moving horizontally with a velocity 50 $m s^{- 1}$ . A mass of 250 kg is added. Find the final velocity.
A $40 m s^{- 1}$
B $23 m s^{- 1}$
C $12 m s^{- 1}$
D $12.5 m s^{- 1}$
A marble block of mass 2 kg lying on ice when given a velocity of $6 m s^{- 1}$ is stopped by friction in 10 s. Then the coefficient of friction is $(g = 10 m s^{- 2})$
A0.02
B0.03
C0.06
D0.01
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is $v_{1}$ and velocity of second ball after collision is $v_{2}$ then
A $v_{1} = \frac{(1 - e) u}{2}, v_{2} = \frac{(1 + e) u}{2}$
B $v_{1} = \frac{(1 + e) u}{2}, v_{2} = \frac{(1 - e) u}{2}$
C $v_{1} = \frac{u}{2}, v_{2} = - \frac{u}{2}$
D $v_{1} = (1 + e) u, v_{2} = (1 - e) u$