PQR is a triangle right angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
Step by step video & image solution for PQR is a triangle right angled at P and M is a point on QR such that P M_|_Q R. Show thatP M^2=Q MdotM R. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SHORT ANSWER (SA-II) TYPE QUESTIONS
21 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
- TRIANGLESBOOK - EDUCART PUBLICATIONCHAPTER - TRIANGLESEXERCISE - VERY SHORT QUESTIONS
10 Videos
- SURFACE AREAS AND VOLUMESBOOK - EDUCART PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
30 Videos
Similar Questions
Knowledge Check
The vertices of a right angled triangle right angle at P are P (3,4) , Q(7,4) and R (3,8). Then, what is the coordinates of orthocentre of ΔPQR ?
A(3,4)B(7,4)C(3,8)D(5,6)In a ∠PQR, M lies on PR and between P and R such that QR=QM=PM. If ∠MQR=40∘, then find ∠P.
A35∘B25∘C45∘D55∘
PQRS is a trapezium having PS a n d QR as parallel sides. A is any point on PQandB is a point on SR such that ABQR . If area of PBQ is 17cm2, find the area of ASR
View SolutionIn a triangle PQR, right angled at Q. PQ=5 cm, QR=12 cm. Find the length of QM , if M is the mid point of PR .
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View SolutionIf in a triangle PQR;sinP,sinQ,sinR are in A.P; then
View Solution1. Let PQR be a right angled isosceles triangle, right angled at P (2,1). If the equation of the line QR is 2x + y 3, then the equation representing the pair of (1999, 2M) lines P and PR is
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
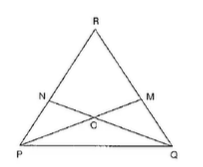
View Solution