Determine the number of multiples of 4 that lie between 10 and 250.
The correct Answer is:60
To determine the number of multiples of 4 that lie between 10 and 250, we can follow these steps:
Step 1: Identify the first multiple of 4 greater than 10
The first multiple of 4 after 10 is 12. (4 x 3 = 12)
Step 2: Identify the last multiple of 4 less than or equal to 250
The last multiple of 4 before 250 is 248. (4 x 62 = 248)
Step 3: Write the sequence of multiples of 4
The multiples of 4 between 10 and 250 can be represented as:
12, 16, 20, ..., 248.
Step 4: Identify the first term (A), common difference (D), and last term (An)
- First term (A) = 12
- Common difference (D) = 4 (since we are counting multiples of 4)
- Last term (An) = 248
Step 5: Use the formula for the nth term of an arithmetic sequence
The formula for the nth term of an arithmetic sequence is given by:
An=A+(N−1)⋅D
Step 6: Substitute the known values into the formula
Substituting the known values:
248=12+(N−1)⋅4
Step 7: Solve for N
1. Rearranging the equation:
248−12=(N−1)⋅4
236=(N−1)⋅4
2. Dividing both sides by 4:
N−1=2364
N−1=59
3. Adding 1 to both sides:
N=59+1
N=60
Conclusion
The number of multiples of 4 that lie between 10 and 250 is 60.
---
The first multiple of 4 after 10 is 12. (4 x 3 = 12)
The last multiple of 4 before 250 is 248. (4 x 62 = 248)
The multiples of 4 between 10 and 250 can be represented as:
12, 16, 20, ..., 248.
- First term (A) = 12
- Common difference (D) = 4 (since we are counting multiples of 4)
- Last term (An) = 248
The formula for the nth term of an arithmetic sequence is given by:
An=A+(N−1)⋅D
Substituting the known values:
248=12+(N−1)⋅4
1. Rearranging the equation:
248−12=(N−1)⋅4
236=(N−1)⋅4
N−1=2364
N−1=59
N=59+1
N=60
The number of multiples of 4 that lie between 10 and 250 is 60.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - A (SECTION - II)20videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - B (SECTION - III)8videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C10videos
SAMPLE PAPER 5
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-B(SECTION-V)5videos
SAMPLE PAPER 4
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- C10videos
SAMPLE PAPER 6
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of student, whose marks lie between 40.5 and 50.5 is
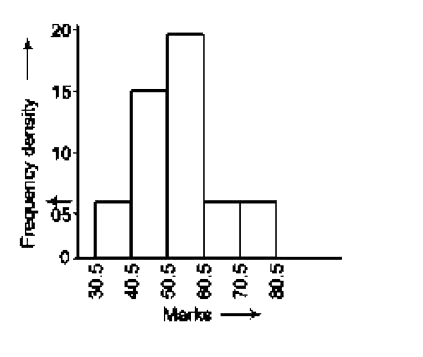 A15B10C5DNone of these
A15B10C5DNone of these
How many multiple of 4 lie between 10 and 250 ?
View SolutionHow many multiples of 4 lie between 10 and 205?
View SolutionHow many multiples of 5 lie between 50 and 250?
View SolutionDetermine the lowest common multiple of 6 and 9.
View Solution5-digit numbers are to be formed using 2,3,4,5,7,9 without repeating the digits. If p be the number of such numbers that exceed 20000and q be the number ofthose that lie between 30000 and 90000, then p:q is
View SolutionFind the number of integers which lie between 1 and 106 and which have the sum of the digits equal to 12.
View SolutionWhich of the following numbers does not lie between -1 and -2?
View Solution

