Find the mean of the following distribution:
x1030507090f751035
The correct Answer is:49
To find the mean of the given distribution, we will follow these steps:
Step 1: Write down the data
We have the following values:
- x=(10,30,50,70,90)
- f=(7,5,10,3,5)
Step 2: Calculate f⋅x
We need to multiply each value of x by its corresponding frequency f:
- For x=10 and f=7:
f⋅x=10⋅7=70
- For x=30 and f=5:
f⋅x=30⋅5=150
- For x=50 and f=10:
f⋅x=50⋅10=500
- For x=70 and f=3:
f⋅x=70⋅3=210
- For x=90 and f=5:
f⋅x=90⋅5=450
Now we can summarize these calculations:
f⋅x=(70,150,500,210,450)
Step 3: Calculate Σf⋅x
Now we will sum up all the values of f⋅x:
Σf⋅x=70+150+500+210+450
Calculating this step-by-step:
- 70+150=220
- 220+500=720
- 720+210=930
- 930+450=1380
So, Σf⋅x=1380.
Step 4: Calculate Σf
Now we will sum up the frequencies f:
Σf=7+5+10+3+5
Calculating this:
- 7+5=12
- 12+10=22
- 22+3=25
- 25+5=30
So, Σf=30.
Step 5: Calculate the mean
Now we can calculate the mean using the formula:
¯x=Σf⋅xΣf=138030
Calculating this:
¯x=46
Final Answer
The mean of the distribution is 46.
---
We have the following values:
- x=(10,30,50,70,90)
- f=(7,5,10,3,5)
We need to multiply each value of x by its corresponding frequency f:
- For x=10 and f=7:
f⋅x=10⋅7=70
- For x=30 and f=5:
f⋅x=30⋅5=150
- For x=50 and f=10:
f⋅x=50⋅10=500
- For x=70 and f=3:
f⋅x=70⋅3=210
- For x=90 and f=5:
f⋅x=90⋅5=450
f⋅x=(70,150,500,210,450)
Now we will sum up all the values of f⋅x:
Σf⋅x=70+150+500+210+450
Calculating this step-by-step:
- 70+150=220
- 220+500=720
- 720+210=930
- 930+450=1380
Now we will sum up the frequencies f:
Σf=7+5+10+3+5
Calculating this:
- 7+5=12
- 12+10=22
- 22+3=25
- 25+5=30
Now we can calculate the mean using the formula:
¯x=Σf⋅xΣf=138030
Calculating this:
¯x=46
The mean of the distribution is 46.
Topper's Solved these Questions
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - A (SECTION - II)
20 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - PART - B (SECTION - III)
8 Videos
- SAMPLE PAPER 5BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5EXERCISE - SECTION - C
10 Videos
- SAMPLE PAPER 4BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4EXERCISE - PART-B(SECTION-V)
5 Videos
- SAMPLE PAPER 6BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- C
10 Videos
Similar Questions
Find the mean of the following distribution
X:4691015F:5101078
View SolutionFind the mean of the following distribution: x: 10 30 50 70 89 f: 7 8 10 15 10
View SolutionFind the mean of the following distribution: 10 30 50 70 89 7 8 10 15 10
View SolutionFind the mean of the following distribution: 4 6 9 10 15 5 10 10 7 8
View SolutionFind the median of the following distribution:
xf xf102 304203 405506 803605 903704 1001
View SolutionFind the mean of the following distribution: x: 4 6 9 10 15 f: 5 10 10 7 8
View SolutionFind the value of if the mean of the following distribution is 7.5
View SolutionFind the value of p, if mean of the following distribution is 7.5.
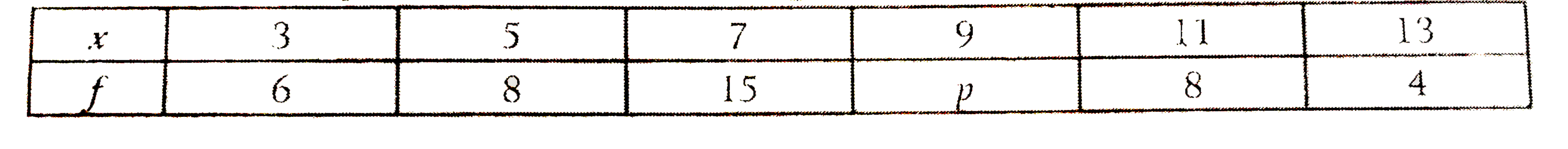
View SolutionFind the mean of the following frequency distribution:
Class0−55−1010−1515−2020−2525−30Frequency122672
View SolutionCalculate mean deviation from the median for the following distribution: xi: , 10, 15, 20, 25, 30, 35, 40, 45 fi: , 7, 3, 8, 5, 6, 8, 4, 9
View Solution
