Question

State Kirchhoff's law for an electrical network: Using these laws deduce the condition for balance in a Wheatstone bridge.

Explanation

Kirchhoff.s Laws :
(i) Function rule : At any junction the sum of currents towords the junction is equal to sum of currents away from the junction . (OR) Alzebraic sum of currents around a junction is zero.
(ii) Loop rule : Alzebraic sum of changes in potential around any closed loop involving resistors and cells in the loop is zero.
Applying Kirchhoff.s Law to a Wheatstone bridge : Wheatstone bridge consists of four resistances P, Q,R, S Connected as shown in the figure and are referred as arms of the bridge.

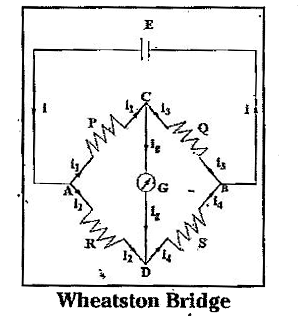
A battery of emf .E. is connected between two junctions A and B and a galvanometer of resistance .G. is connected between .C. and .D.,
Applying Kirchhoff.s first law,
at the junction C, `i_(1)=i_(g)+i_(3).......(1)`
at the junction D, `i_(2)+ i_(g)= i_(4).......(2)`
Applying Kirchhoff.s Second law for the loop ACDA
`i_(1)" p " i_(g)" G "+i_(2)R=0......(3)`
For the loop CBDC,
`i_(3)" Q " +i_(4)S+i_(g)G=0`
If no current passes through the galvanometer then the bridge is said to be balanced.
So, `i_(g)=0,` then (1),(2),(3)and (4) becomes.
`i_(1)=i_(3),i_(2)=i_(4)," "i_(1)P=i_(2)R" and "i_(3) Q=i_(4) S.`
By adjusting the above equations we get `(P)/(Q)=(R)/(S).`
This is the balancing conditions of a Wheatstones bridge.