In a potential meter arrangement shown in fig. The balancing length for potential difference across X,Y points is found to be 45.5 cm. Then the balancing length for potential difference across ( Y ) and ( Z) would be

A
45.50 cm
B
56.87cm
C
36.40 cm
D
none of the above
Video Solution
Text Solution
The correct Answer is:C
Determine the value of potential gradient for the given potentiometer bridge,
And also take ratio of potential drop across both the resistance. That can be written as,
V1V2=R1R2=L1L2 where V1,V2,R1,R2,L1&L2 represents voltage across 5Ω , voltage across 4 Ω , value of first resistance, value of second resistance, balancing point for first resistance and balancing point of second resistance respectively.
⇒54=45.5L2
⇒L2=45.5×45
L2=36.4 cm
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In a potentiometer arrangement shown in fig. The balancing length for p.d. across xy points is found to be 45.5cm. Then the balancing length for p.d. across (Y) and (Z) would be
(##MOT_CON_NEET_PHY_C22_E02_010_Q01.png" width="80%">A45.50cmB56.87cmC36.40cmDnone of the above - Question 2 - Select One
Find the potential difference across C2.
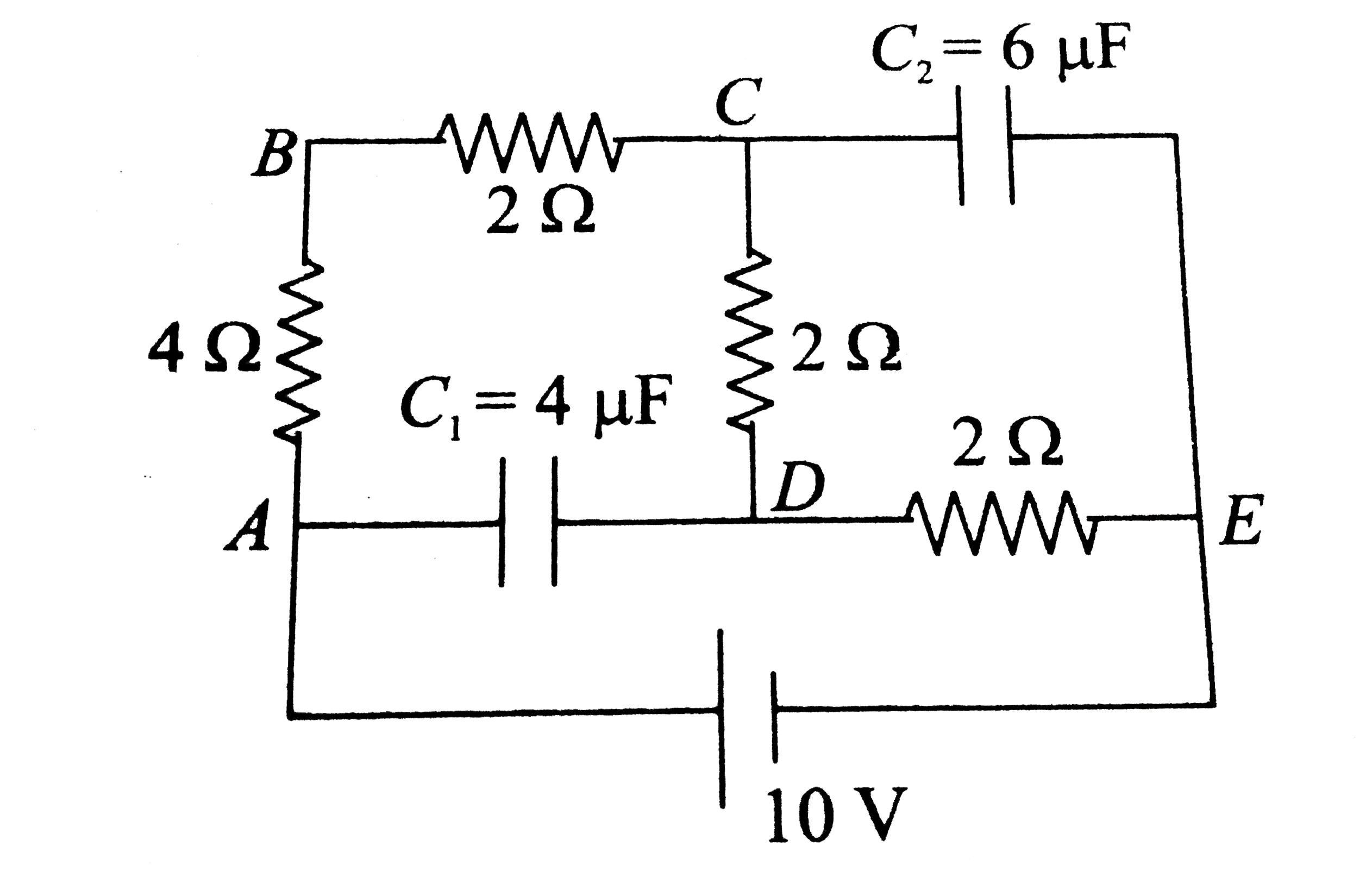 A6 VB4 VCzeroD2 V
A6 VB4 VCzeroD2 V - Question 3 - Select One
An unknown resistance R is connected in series with a 2 ohm resistance. A current is flowing in this combination. The balancing length for potential difference across 2 ohm resistor, in a potentiometer experiment is found to be 300 cm, while the balancing length for the potential difference across the unknown R is found to be 360cm. The unknown resistance R is
A2.4 ohmB3.0 ohmC3.6 ohmD6.6 ohm
Potential difference across AB in the network shown is
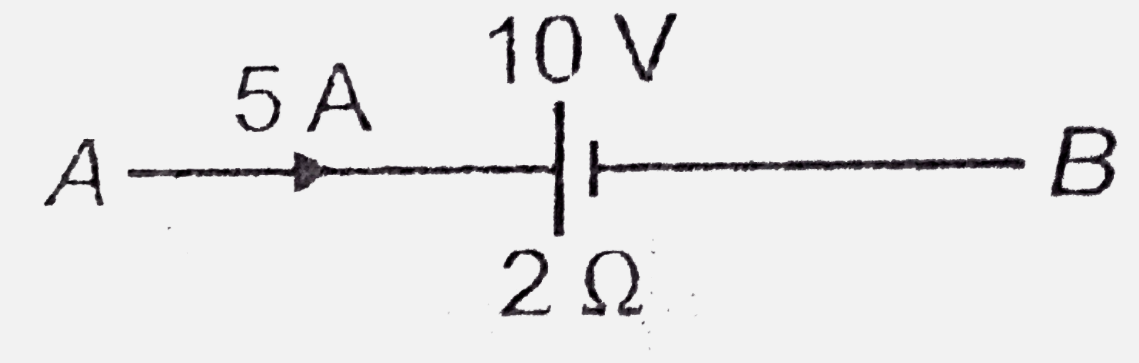 View Solution
View SolutionPotential difference across AB in the network shown is
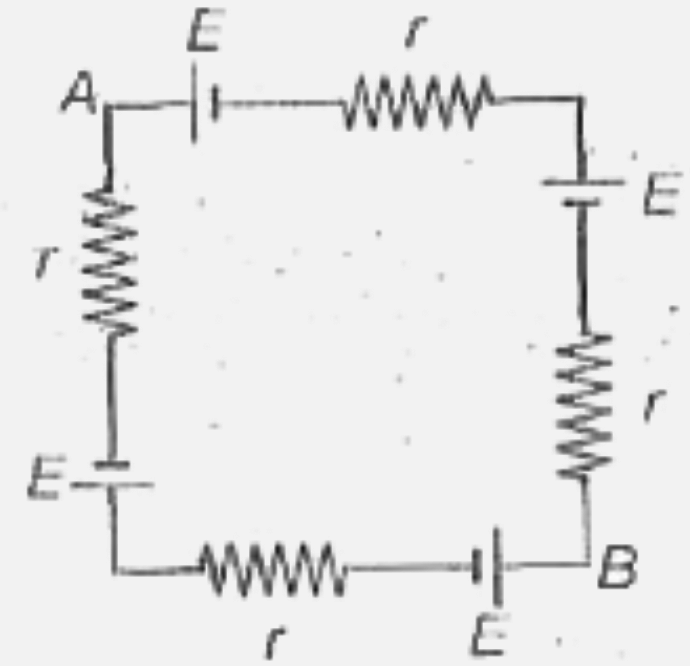 View Solution
View SolutionPotential difference across AB in the network shown is
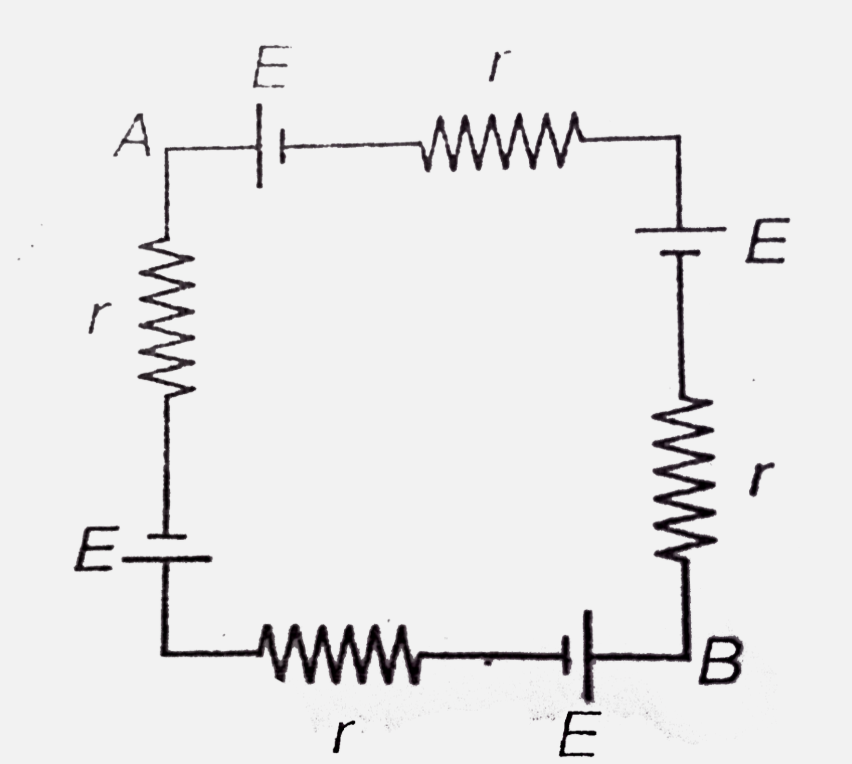 View Solution
View SolutionIn the network shown below , potential difference across CD is
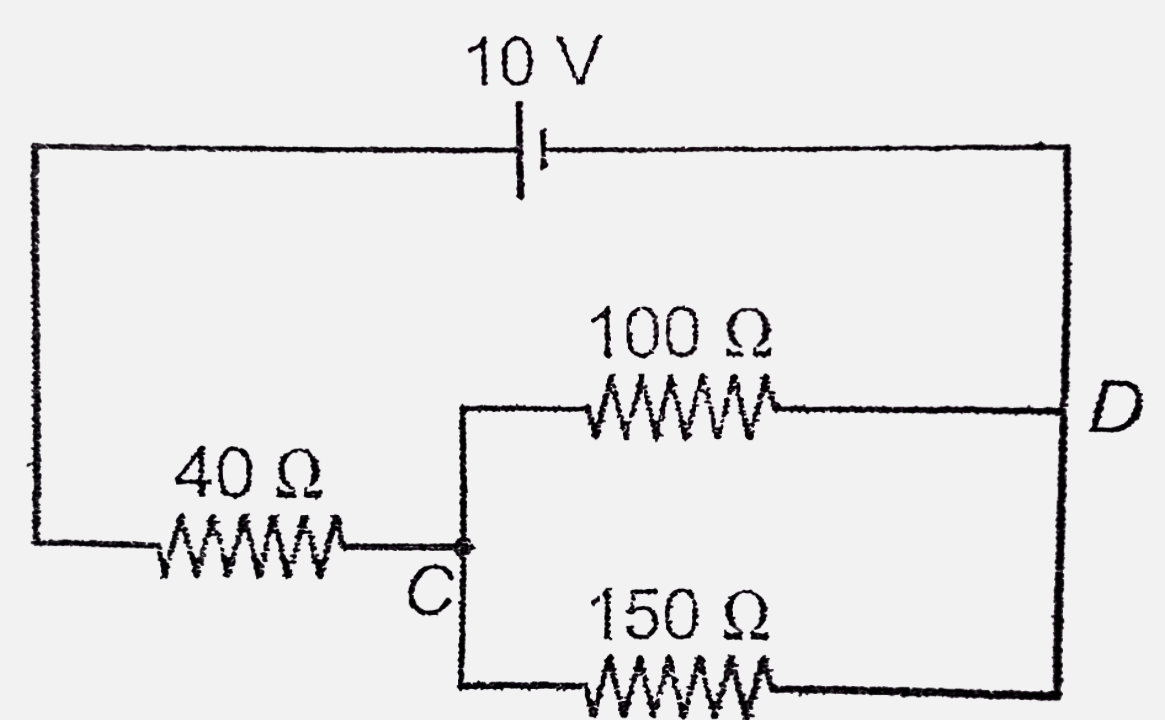 View Solution
View SolutionThe potential difference across 4Ω will be.
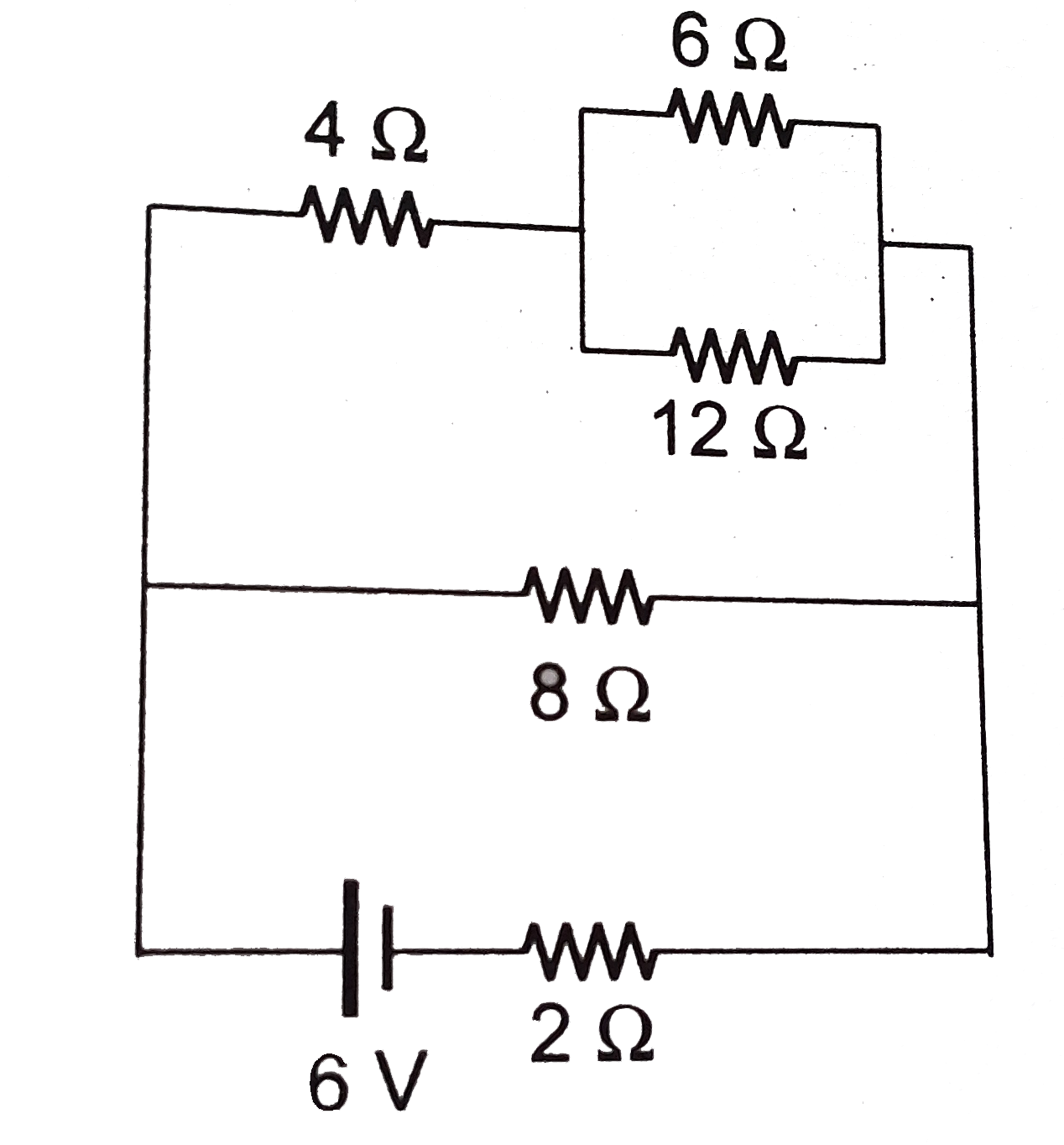 .View Solution
.View Solution

