A small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
0.4 cm
2.4 cm
1.8 cm
1.2 cm
The correct Answer is:A
The situation can be shown as:
Let radius of complete disc is a and that of small disc is b also let centre of mass now shifts to O2 at a distance x, from original centre.
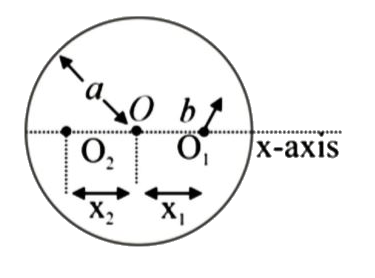
The position of new centre of mass is given by:
XCM=σ.πb2.x1σ.πa2−σ.πb2
Here, a = 6 cm, b = 2 cm, x1=3.2cm
Hence, XCM=−σ×π(2)2×3.2σ×π×(6)2−σ×π×(2)2
=12.8π32π=0.4cm
Topper's Solved these Questions
Similar Questions
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion
View SolutionA small disc of radius 6 cm. If the distance between their centres is 3.2 cm, what is the shift in the centre of mass of the disc ?
View Solution
Knowledge Check
A small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
A0.4 cmB2.4 cmC1.8 cmD1.2 cmA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
A0.4mB2.4cmC1.8cmD1.2cmA small disc of radius 6 cm. If the distance between their centres is 3.2 cm, what is the shift in the centre of mass of the disc ?
A0.4 cmB2.4 cmC1.8 cmD1.2 cm
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionIn the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6π at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :

View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
View SolutionGiven a uniform disc of mass M and radius R. A small disc of radius R/2 is cut from this disc in such a way that the distance between the centres of the two discs is R/2. Find the moment of inertia of the remaining disc about a diameter of the original disc perpendicular to the line connecting the centres of the two discs
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the cirucmferences of the discs coincide. The centre of mass of the new disc is αR from the center of the bigger disc. The value of α is
View Solution
