One - fourth length of a uniform rod is placed on a rough horizontal surface and it starts rotating about the edge as soon as we release it. The rod starts slipping on the edge when it has turned through an angle θ. If the coefficient of friction between rod and surface is μ, and it satisfies the relation xtanθ=4μ, then what is the value of x? [Take g=10m/s2]
The correct Answer is:13
mgl4sinθ=12Iω2
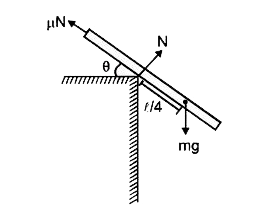
μN−mgsinθ=mω214
mgcosθ−N=m14α
Solving,
13tanθ=4μ
⇒x=13
Topper's Solved these Questions
Similar Questions
One fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.

View SolutionA uniform rod of length 2a is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance a/3 from the edge. The rod is released from rest. If the rod slips after it turned an angle θ, find the coefficient of friction between the rod and the table.
View Solution
Knowledge Check
A uniform metal chain is placed on a rough table such that the one end of chain hangs down over the edge of the table, when one-third of its length hang over the edge, the chain starts sliding. Then the coefficient of static friction is
A34B14C23D12A horizontal force is applied on a body on a rough horizontal surface produces an acceleration ‘a’. If coefficient of friction between the body and surface which is μ is reduced to μ/3, the acceleration increases by 2 units. The value of 'μ' is
A2/3gB3/2gC3/gD1/g
A rod of mass M and length L lies on an incline having inclination of θ=37∘. The coefficient of friction between the rod and the incline surface is μ=0.90. Find the tension at the mid point of the rod.
View Solution
One-fourth length of a uniform rod of mass m and length l is placed on a rough horizontal surface and it is held stationary in horizontal position by means of a light thread as shown in the figure. The thread is then burnt and the rod start rotating about the edge. Find the angle between the rod and the horizontal when it is about to slide on the edge. The coefficient of friction between the rod and surface is μ.
View SolutionA uniform rod of length L and mass M has been placed on a rough horizontal surface. The horizontal force F applied on the rod is such that the rod is just in the state of rest. If the coefficient of friction varies according to the relation μ =Kx where K is a +ve constant. Then the tension at mid point of rod is?
View SolutionA uniform rod of length l is kept vertically on a rough horizontal surface at x = 0 . It is rotated slightly and released . When the rod finally falls on the horizontal surface , the lower end will remain at

View SolutionA uniform rod of length 1m lies on the smooth part of a horizontal surface as shown. Calculate the minimum veloctiy V0 in m/s so that the rod can reach the rough surface completely. Take g=10m/s2 and coefficient of friction between the rod and the rough surface as 0.1.

View SolutionA conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
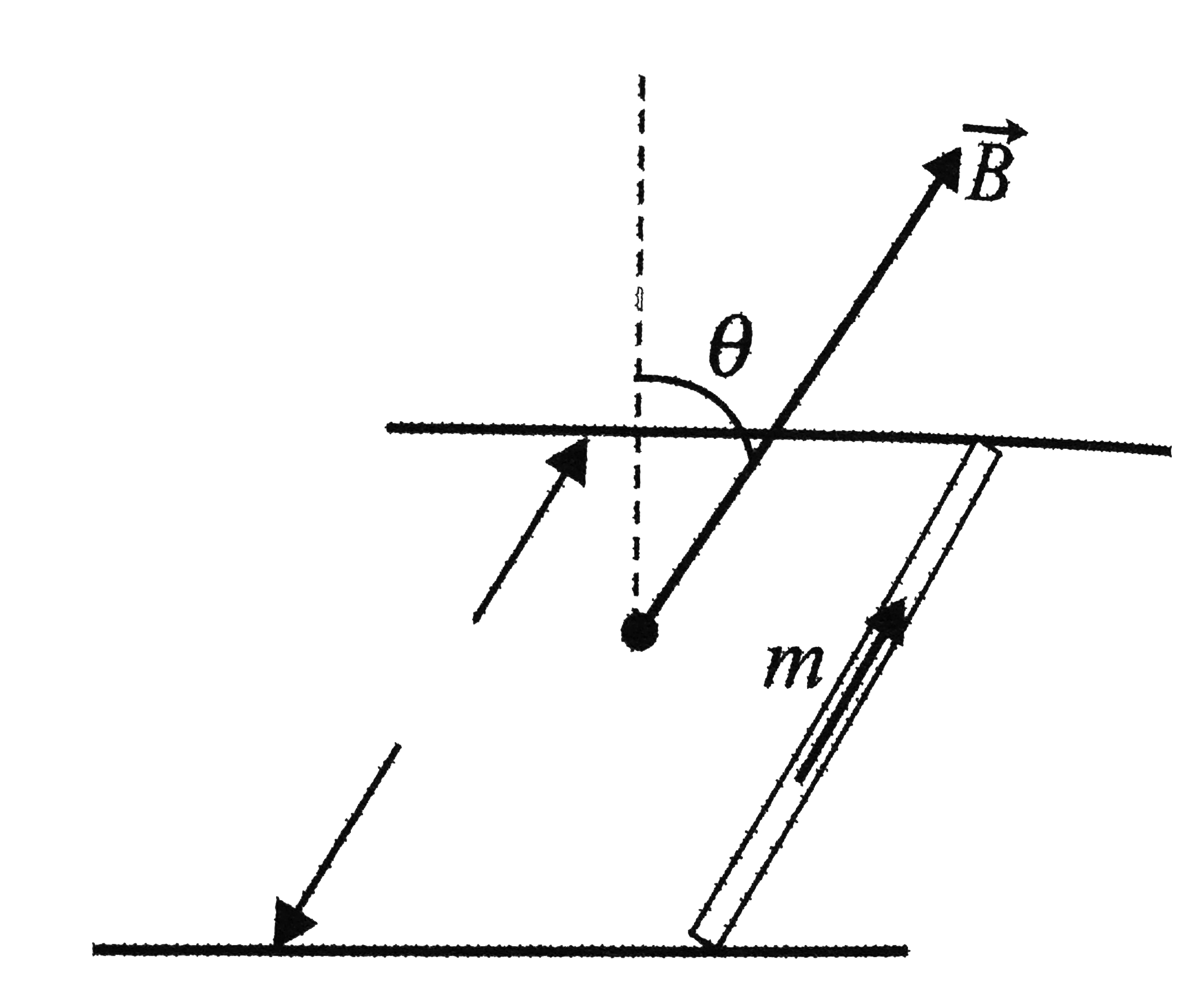
View Solution
