Density of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
Which of the following has maximum density?
O2 at 25∘ C and 1 atm
O2 at 0∘ C and 2 atm
O2 at 273∘C and 1 atm
O2 at 0∘ C and 1 atm
To determine which gas has the maximum density among the given options, we will use the formula for density derived from the ideal gas equation. The steps are as follows:
Step 1: Understand the Density Formula
The density (d) of a gas can be expressed using the formula:
d=PMRT
where:
- P = pressure of the gas
- M = molar mass of the gas
- R = universal gas constant
- T = absolute temperature in Kelvin
Step 2: Identify Constants
Since we are comparing the density of oxygen gas in different conditions, the molar mass (M) and the gas constant (R) will remain constant for all cases. Therefore, the density will depend on the ratio of pressure (P) to temperature (T):
d∝PT
Step 3: Analyze the Given Conditions
We have the following conditions for oxygen:
1. 25°C and 1 atm
2. 0°C and 2 atm
3. 273°C and 1 atm
4. 0°C and 1 atm
We need to convert the temperatures from Celsius to Kelvin:
- 25°C = 298 K
- 0°C = 273 K
- 273°C = 546 K
Now, we can summarize the conditions:
1. P1=1atm,T1=298K
2. P2=2atm,T2=273K
3. P3=1atm,T3=546K
4. P4=1atm,T4=273K
Step 4: Calculate the Density Ratio for Each Condition
Using the formula d∝PT, we can calculate the density ratios:
1. For condition 1: P1T1=1298
2. For condition 2: P2T2=2273
3. For condition 3: P3T3=1546
4. For condition 4: P4T4=1273
Step 5: Compare the Ratios
To find which condition has the maximum density, we need to compare the values of PT:
1. 1298≈0.00336
2. 2273≈0.00734
3. 1546≈0.00183
4. 1273≈0.00366
Step 6: Conclusion
From the calculated ratios, we see that:
- Condition 2 (0°C and 2 atm) has the highest ratio PT.
Thus, the maximum density is found in condition 2.
Final Answer
The option with maximum density is Condition 2: 0°C and 2 atm.
The density (d) of a gas can be expressed using the formula:
d=PMRT
where:
- P = pressure of the gas
- M = molar mass of the gas
- R = universal gas constant
- T = absolute temperature in Kelvin
Since we are comparing the density of oxygen gas in different conditions, the molar mass (M) and the gas constant (R) will remain constant for all cases. Therefore, the density will depend on the ratio of pressure (P) to temperature (T):
d∝PT
We have the following conditions for oxygen:
1. 25°C and 1 atm
2. 0°C and 2 atm
3. 273°C and 1 atm
4. 0°C and 1 atm
- 25°C = 298 K
- 0°C = 273 K
- 273°C = 546 K
1. P1=1atm,T1=298K
2. P2=2atm,T2=273K
3. P3=1atm,T3=546K
4. P4=1atm,T4=273K
Using the formula d∝PT, we can calculate the density ratios:
1. For condition 1: P1T1=1298
2. For condition 2: P2T2=2273
3. For condition 3: P3T3=1546
4. For condition 4: P4T4=1273
To find which condition has the maximum density, we need to compare the values of PT:
1. 1298≈0.00336
2. 2273≈0.00734
3. 1546≈0.00183
4. 1273≈0.00366
From the calculated ratios, we see that:
- Condition 2 (0°C and 2 atm) has the highest ratio PT.
Thus, the maximum density is found in condition 2.
The option with maximum density is Condition 2: 0°C and 2 atm.
Similar Questions
Density of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
The density of CO2 at 1 atm and 273K is
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
The density of gas is 3.8 g L−1 at STP. The density at 27°C and 700 mm Hg pressure will be
View SolutionAt a constant temperature what is the relation between pressure P density d of an ideal gas ?
View SolutionUsing the equation of state pV=nRT, show that at a given temperature the density of gas is proportional to gas pressure p.
View SolutionFor V versus T curves at constant pressure P1andP2 for and ideal gas shown in figure-
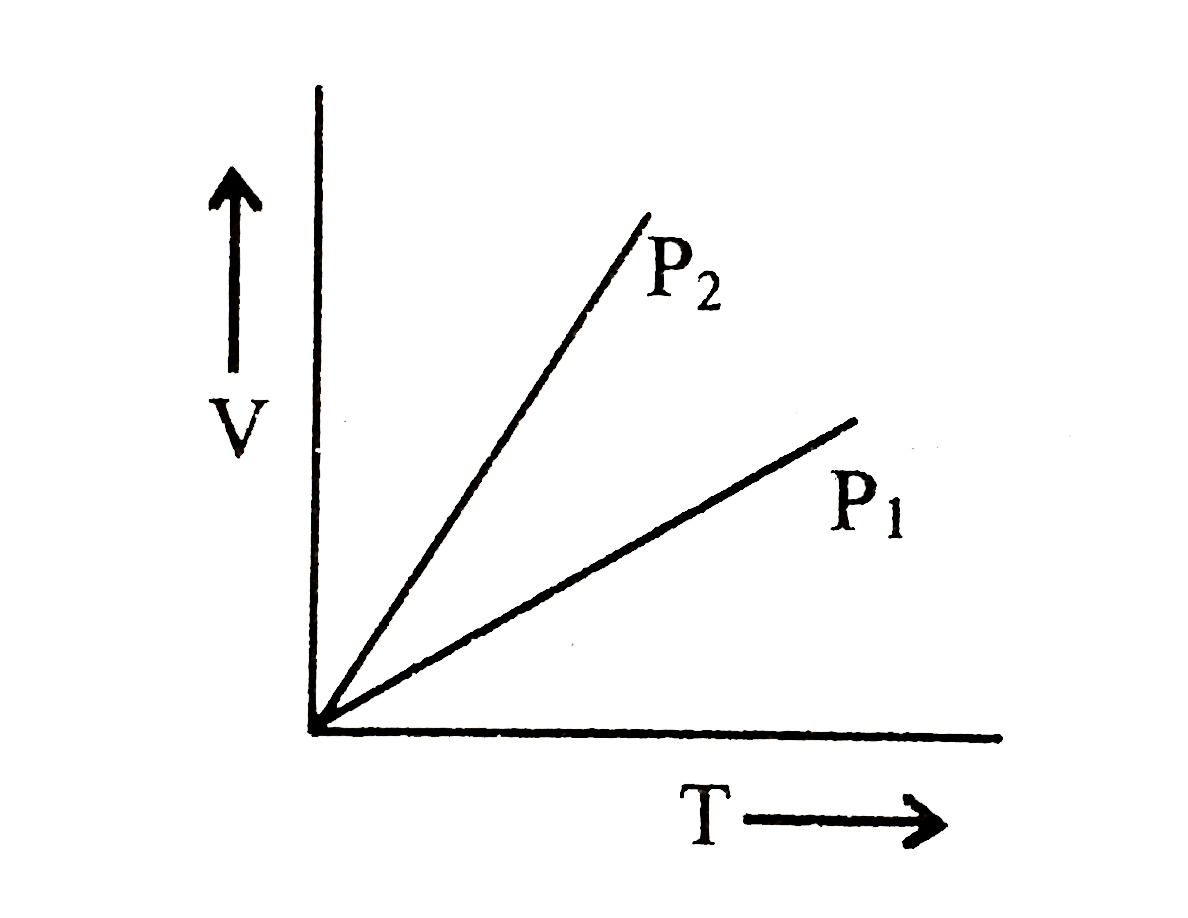
View SolutionThe ideal gas equation for 1 mol of ideal gas is PV = nRT
graph between P and T at constant volume, i.e. isochores are plotted as under

Which of the following order of volume is correct ?
View SolutionIn a dilute gas at pressure P and temperature T, the mean time between successive collisions of a molecule varies with T as :
View SolutionDuring an experiment, an ideal gas is found to obey a condition p2ρ=constant. (ρ = density of the gas). The gas is initially at temperature (T), pressure (p) and density ρ. The gas expands such that density changes to ρ/2.
View SolutionDuring an experiment, an ideal gas is found to obey a condition p2ρ=constant. (ρ = density of the gas). The gas is initially at temperature (T), pressure (p) and density ρ. The gas expands such that density changes to ρ/2.
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
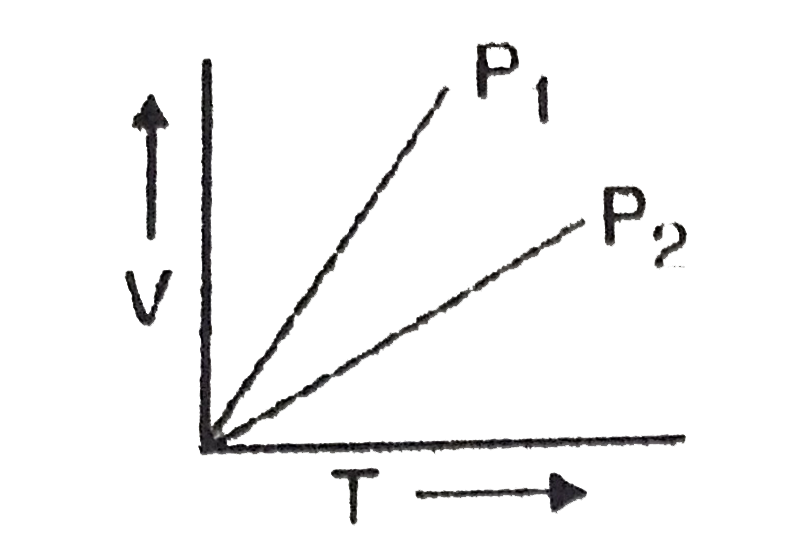
Which is correct ?
View Solution
