Density of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
The density of CO2 at 1 atm and 273K is
1.96gL−1
2.12gL−1
1.09gL−1
2.02gL−1
Step by step video & image solution for Density of gas is inversely proportional to absolute temperature and directly proportional to pressure rArr d prop P/T rArr (dT)/P = constant rArr (d_(1)T_(1))/P_(1) =(d_(2)T_(2))/P_(2) Density at a particular temperature and pressure can be calculated bousing ideal gas equation PV = nRT rArr PV = ("mass")/("molar mass (M)") x RT P xx M =("mass")/("volume") xx RT rArr P xx M = d xx RT d=(PM)/(RT) The density of CO_2 at 1 atm and 273K is by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Density of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
The density of gas is 3.8 g L−1 at STP. The density at 27°C and 700 mm Hg pressure will be
View SolutionDensity of gas is inversely proportional to absolute temperature and directly proportional to pressure
⇒d∝PT⇒dTP = constant ⇒d1T1P1=d2T2P2
Density at a particular temperature and pressure can be calculated bousing ideal gas equation
PV=nRT⇒PV=massmolar mass (M)xRT
P×M=massvolume×RT⇒P×M=d×RT
d=PMRT
Which of the following has maximum density?
View SolutionAt a constant temperature what is the relation between pressure P density d of an ideal gas ?
View SolutionUsing the equation of state pV=nRT, show that at a given temperature the density of gas is proportional to gas pressure p.
View SolutionFor V versus T curves at constant pressure P1andP2 for and ideal gas shown in figure-
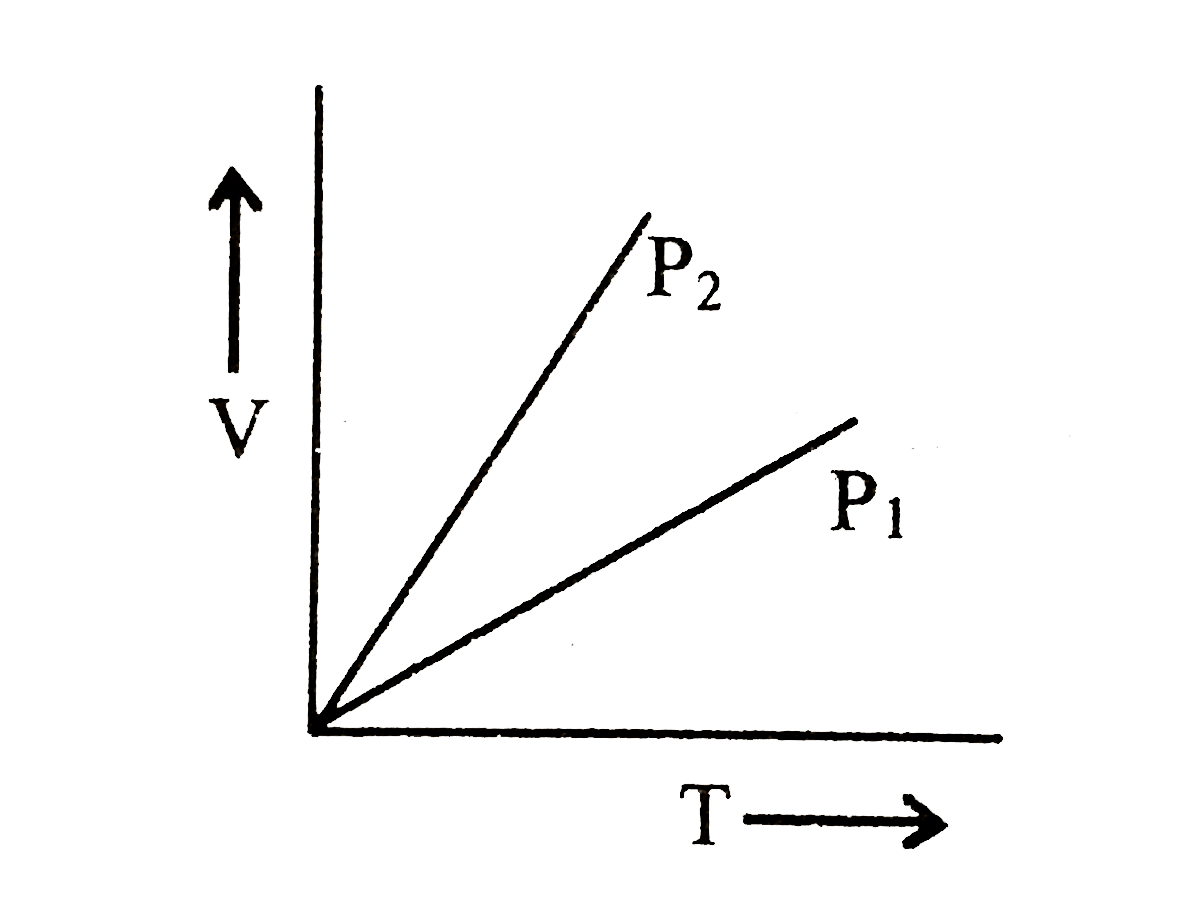
View SolutionIn a dilute gas at pressure P and temperature T, the mean time between successive collisions of a molecule varies with T as :
View SolutionDuring an experiment, an ideal gas is found to obey a condition p2ρ=constant. (ρ = density of the gas). The gas is initially at temperature (T), pressure (p) and density ρ. The gas expands such that density changes to ρ/2.
View SolutionDuring an experiment, an ideal gas is found to obey a condition p2ρ=constant. (ρ = density of the gas). The gas is initially at temperature (T), pressure (p) and density ρ. The gas expands such that density changes to ρ/2.
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
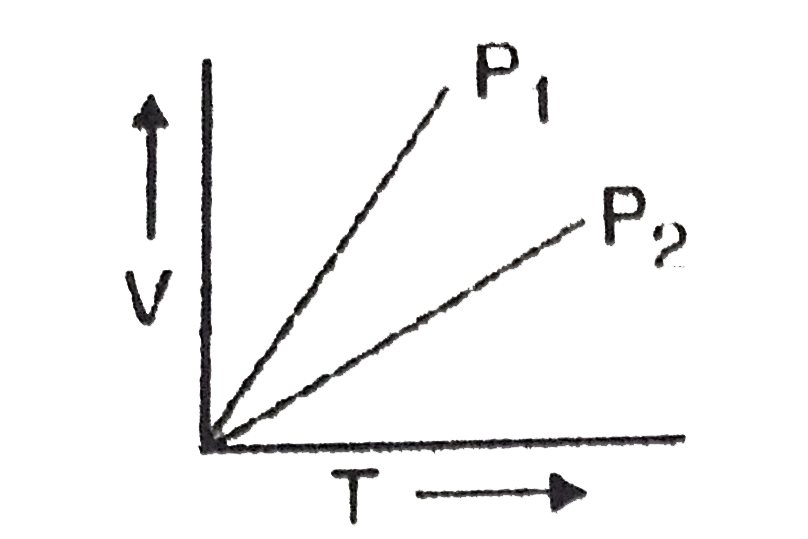
Which is correct ?
View SolutionA vessel contains 1 mole of O2 gas (molar mass 32) at a temperature T. The pressure of the gas is P . An identical vessel containing one mole of He gas (molar mass 4) at a temperature 2T has a pressure of xP. Find the value of x.
View Solution
