A bullet fired vertically up from the ground reaches a point in its path after 3s and 13 s, both times being taken from the instant of firing the bullet. The velocity of projection of the bullet is (g=10ms−2)
80ms−1
40ms−1
160ms−1
20ms−1
The correct Answer is:A
To find the velocity of projection of the bullet, we can use the information given in the problem. The bullet reaches a certain point in its path at two different times: 3 seconds and 13 seconds after being fired. We also know that the acceleration due to gravity (g) is 10 m/s².
1. Identify the times:
- Let t1=3 seconds
- Let t2=13 seconds
2. Use the formula for velocity of projection:
The formula relating the initial velocity (u), gravity (g), and the times at which the bullet reaches the same height is:
u=g2(t1+t2)
3. Substitute the values into the formula:
- Substitute g=10m/s2, t1=3s, and t2=13s:
u=102(3+13)
4. Calculate the sum of times:
- Calculate t1+t2:
t1+t2=3+13=16s
5. Calculate the initial velocity:
- Now substitute back into the equation:
u=102×16
u=5×16=80m/s
6. Final result:
- The velocity of projection of the bullet is 80m/s.
Final Answer:
The velocity of projection of the bullet is 80m/s.
- Let t1=3 seconds
- Let t2=13 seconds
The formula relating the initial velocity (u), gravity (g), and the times at which the bullet reaches the same height is:
u=g2(t1+t2)
- Substitute g=10m/s2, t1=3s, and t2=13s:
u=102(3+13)
- Calculate t1+t2:
t1+t2=3+13=16s
- Now substitute back into the equation:
u=102×16
u=5×16=80m/s
- The velocity of projection of the bullet is 80m/s.
The velocity of projection of the bullet is 80m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - problems
47 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - Numerical exercise(LEVEL-1)
22 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -II
80 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
Similar Questions
A bullet fired vertically up from the ground reaches a height 40 m in its path from the ground and it takes further time 2 seconds to reach the same point during descent. The total time of flight is (g=10ms−2)
View SolutionA body projected up reaches a point A in its path at the end of 4th second and reaches the ground after 5 seconds from the start. The height of A above the ground is (g=10m/s2)
View SolutionA stone is projected vertically up from the ground with velocity 40ms−1 . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g=10ms−2)
View SolutionA body projected from the ground reaches a point 'X' in its path after 3 seconds and from there it reaches the ground after further 6 seconds. The vertical distance of the point 'X' from the ground is (acceleration due to gravity =10ms−2)
View SolutionA rocket is fired vertically from the ground. It moves upwards with a constant acceleration 10m/s2 after 30 sec the fuel is finished. After what time from the instant of firing the rocket will attain the maximum height? g=10m/s2:-
View SolutionTwo paper screens A and B are separated by 150m. A bullet pierces A and B. The hole in B in 15 cm below the hole in A. If the bullet is travelling horizontally at the time of hitting A, then the velocity of the bullet at A is: (g=10ms−2)
View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View SolutionA ball is thrown vertically upwards from the ground and a student gazing out of the window sees it moving upward past him at 10ms−1. The window is at 15 m above the ground level. The velocity of ball 3 s after it was projected from the ground is [Take g=10ms−2]
View SolutionA car accelerating at the rate of 2 m/s2 from rest from origin is carrying a man at the rear end who has a gun in his hand. The car is always moving along positive x-axis. At t=4 s, the man fires a bullet from the gun and the bullet hits a bird at t=8s. The bird has a position vector 40ˆi+80ˆj+40ˆk. Find velocity of projection of the bullet. Take the y-axis in the horizontal plane. (g=10m/s2).

View Solution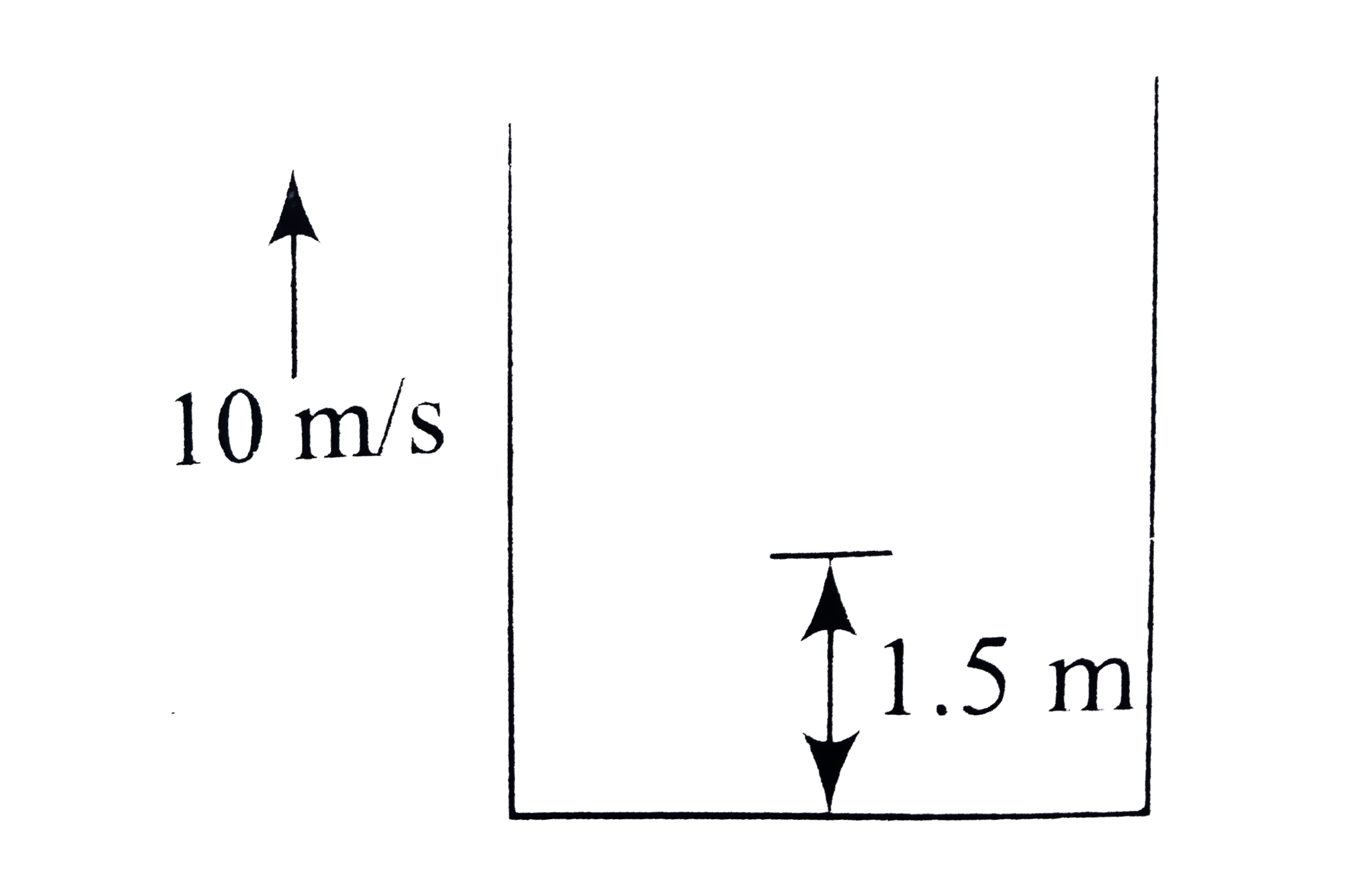
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View Solution
