A body is thrown with the velocity u=12.0ms−1 at an angle of α=45∘ to the horizon. If it touches the ground at the distance s from the point where it was thrown. From what height h should stone be thrown in a horizontal direction with the same initial velocity u so that it falls at the same spot ?
To solve the problem step by step, we will follow the physics of projectile motion and the equations governing it.
Step 1: Determine the Range of the Projectile
The range R of a projectile launched at an angle α with initial velocity u is given by the formula:
R=u2sin(2α)g
Where:
- u=12m/s
- α=45∘
- g=10m/s2 (acceleration due to gravity)
Since sin(90∘)=1, we can substitute the values:
R=122⋅110=14410=14.4m
Step 2: Establish the Horizontal Motion of the Stone
When the stone is thrown horizontally from a height h with the same initial velocity u, the horizontal distance covered will also be R. The time t it takes to fall from height h can be determined using the equation for vertical motion:
h=12gt2
Rearranging gives:
t=√2hg
Step 3: Relate Time and Horizontal Distance
The horizontal distance R covered by the stone thrown horizontally is given by:
R=u⋅t
Substituting t from the previous step:
R=u⋅√2hg
Now substituting R=14.4m and u=12m/s:
14.4=12⋅√2h10
Step 4: Solve for Height h
First, isolate the square root:
√2h10=14.412
Calculating the right side:
√2h10=1.2
Now, square both sides:
2h10=1.22
Calculating 1.22:
2h10=1.44
Now, multiply both sides by 10:
2h=14.4
Finally, divide by 2 to find h:
h=7.2m
Final Answer
The height h from which the stone should be thrown horizontally to land at the same spot is:
7.2m
The range R of a projectile launched at an angle α with initial velocity u is given by the formula:
R=u2sin(2α)g
Where:
- u=12m/s
- α=45∘
- g=10m/s2 (acceleration due to gravity)
R=122⋅110=14410=14.4m
When the stone is thrown horizontally from a height h with the same initial velocity u, the horizontal distance covered will also be R. The time t it takes to fall from height h can be determined using the equation for vertical motion:
h=12gt2
Rearranging gives:
t=√2hg
The horizontal distance R covered by the stone thrown horizontally is given by:
R=u⋅t
Substituting t from the previous step:
R=u⋅√2hg
Now substituting R=14.4m and u=12m/s:
14.4=12⋅√2h10
First, isolate the square root:
√2h10=14.412
Calculating the right side:
√2h10=1.2
Now, square both sides:
2h10=1.22
Calculating 1.22:
2h10=1.44
Now, multiply both sides by 10:
2h=14.4
Finally, divide by 2 to find h:
h=7.2m
The height h from which the stone should be thrown horizontally to land at the same spot is:
7.2m
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - NUMERICAL EXERCISE (LEVEL -2)
19 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
10 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A body is thrown with the velocity 20ms−1 at an angle of 60∘ with the horizontal. Find the time gap between the two positions of the body where the velocity of the body makes an angle of 30∘ with horizontal.
View SolutionA ball is thrown with the velocity u at an angle of α to the horizon. Find (i) the height of which the ball will rise to (ii) the distance x from the point of projection to the point where it reaches to the ground and (iii) the time during which the ball will be in motion (neglect the air resistance ).
View Solution
Knowledge Check
A body is thrown with a velocity of 9.8 m/s making an angle of 30∘ with the horizontal. It will hit the ground after a time
A3 sB2sC1.5 sD1 sA stone is thrown horizontally with velocity u. The velocity of the stone 0.5 s later is 3u/2. The value of u is
A2.2ms−1B3.3ms−1C4.4ms−1D1.1ms−1
A projectile is thrown with initial velocity u0 and angle 30∘ with the horizontal. If it remains in the air for 1s. What was its initial velocity ?
View SolutionAll the particles thrown with same initial velocity would strike the ground.
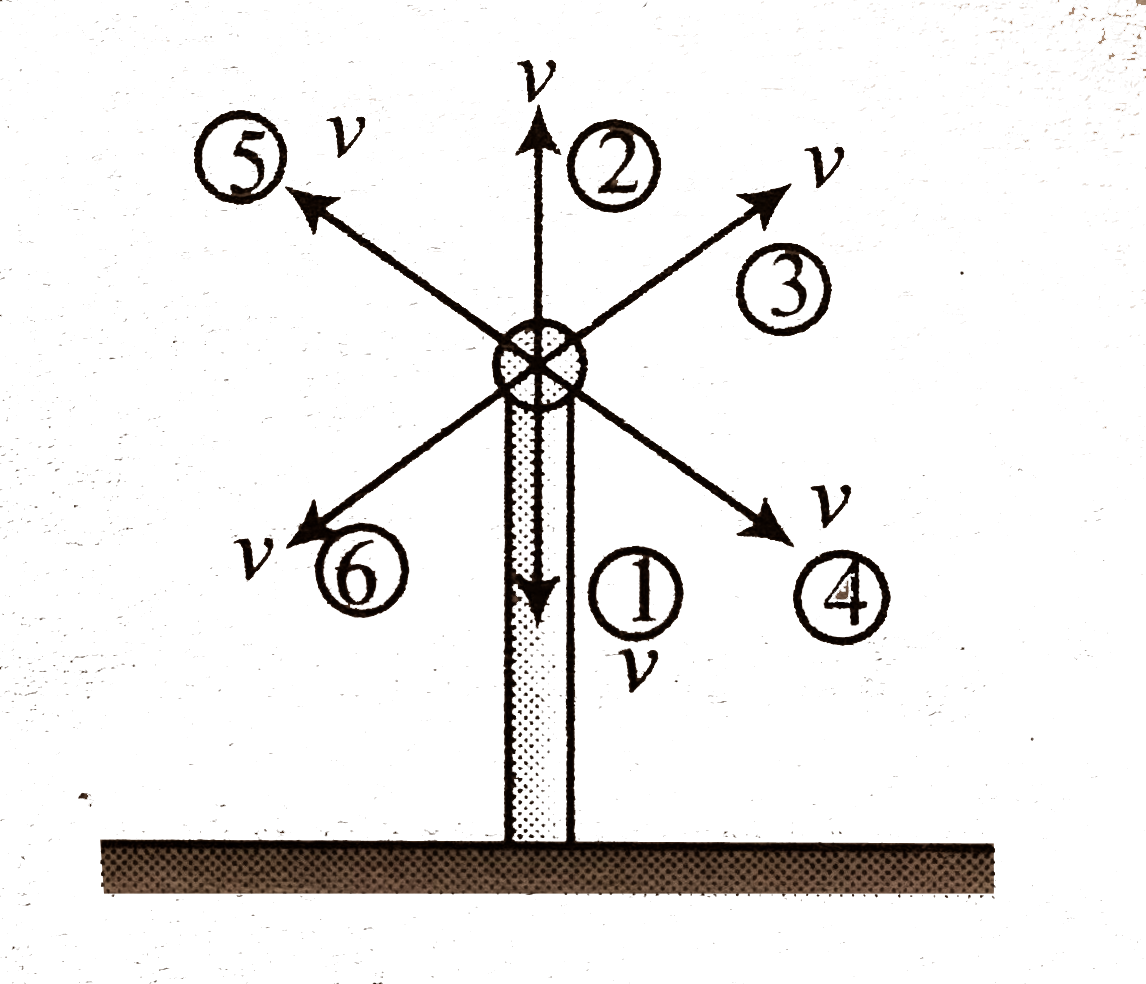 .
.
View SolutionA projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
View SolutionA body is thrown horizontally from the top of a tower of height 5m. It touches the ground at a distance of 10m from the foot of the tower. Find the initial velocity of the body.
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
View Solution
