Rain drops are falling down ward vertically at 4 kmph. For a person,moving forward at 3 kmph feels the rain at
7 kmph
1 kmph
5 kmph
25 kmph
The correct Answer is:C
To find the speed at which the rain appears to fall for a person moving forward, we can break the problem down into steps:
Step 1: Understand the velocities involved
- The rain is falling vertically downward at a speed of 4 km/h.
- The person is moving horizontally forward at a speed of 3 km/h.
Step 2: Represent the velocities as vectors
- Let VR be the velocity of the rain, which is 4km/h downward.
- Let VM be the velocity of the man, which is 3km/h forward.
Step 3: Determine the relative velocity of the rain with respect to the man
- The relative velocity of the rain with respect to the man can be calculated using vector subtraction:
VRM=VR−VM
- Since the rain is falling vertically and the person is moving horizontally, we can visualize this as a right triangle where:
- One side (vertical) represents the velocity of the rain (4km/h).
- The other side (horizontal) represents the velocity of the man (3km/h).
Step 4: Apply the Pythagorean theorem
- To find the resultant velocity VRM, we can use the Pythagorean theorem:
VRM=√(VR)2+(VM)2
VRM=√(4km/h)2+(3km/h)2
VRM=√16+9=√25=5km/h
Step 5: Conclusion
- The speed at which the rain appears to fall for the person moving forward is 5km/h.
- The rain is falling vertically downward at a speed of 4 km/h.
- The person is moving horizontally forward at a speed of 3 km/h.
- Let VR be the velocity of the rain, which is 4km/h downward.
- Let VM be the velocity of the man, which is 3km/h forward.
- The relative velocity of the rain with respect to the man can be calculated using vector subtraction:
VRM=VR−VM
- Since the rain is falling vertically and the person is moving horizontally, we can visualize this as a right triangle where:
- One side (vertical) represents the velocity of the rain (4km/h).
- The other side (horizontal) represents the velocity of the man (3km/h).
- To find the resultant velocity VRM, we can use the Pythagorean theorem:
VRM=√(VR)2+(VM)2
VRM=√(4km/h)2+(3km/h)2
VRM=√16+9=√25=5km/h
- The speed at which the rain appears to fall for the person moving forward is 5km/h.
Similar Questions
Raindrops are falling vertically with a velocity 10m/s. To a cyclist moving on a straight road the rain drops appear to be coming with a velocity of 20m/s. The velocity of cyclist is :-
View SolutionA shower of rain appears to fall vertically downwards with a velocity of 12 kmph on a person walking west wards with a velocity of 5 kmph. The actual velocity and direction of the rain are
View SolutionA man sitting in a bus travelling in a direction from west to east with a speed of 40km/h observes that the rain-drops are falling vertically down. To the another man standing on ground the rain will appear
View SolutionA person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45∘ with the vertical . Find the velocity of rain with respect to the road.
View SolutionA man is walking on a level road at a speed of 3.0 km/h. Rain drops fall vertically with a speed of 4.0 km/h. Find the velocity of the raindrops with respect to the man.
View SolutionWhen a car is at rest, its driver sees rain deops falling on it vertically. When driving the car with spped v, he sees that rain drops are coming at an angle 60∘ from the horizontal. On further increasing the speed of the car to (1+β)v, this angle changes to45∘. The value of β is close to :
View SolutionOn a particular day rain drops are falling vertically at a speed of 5 m/s. A man holdind a plastic board is running to escape from rain as shown. The lower end of board is at a height half that of man and the board makes 45∘ with horizontal. The maximum speed of man so that his feet does not get wet, is
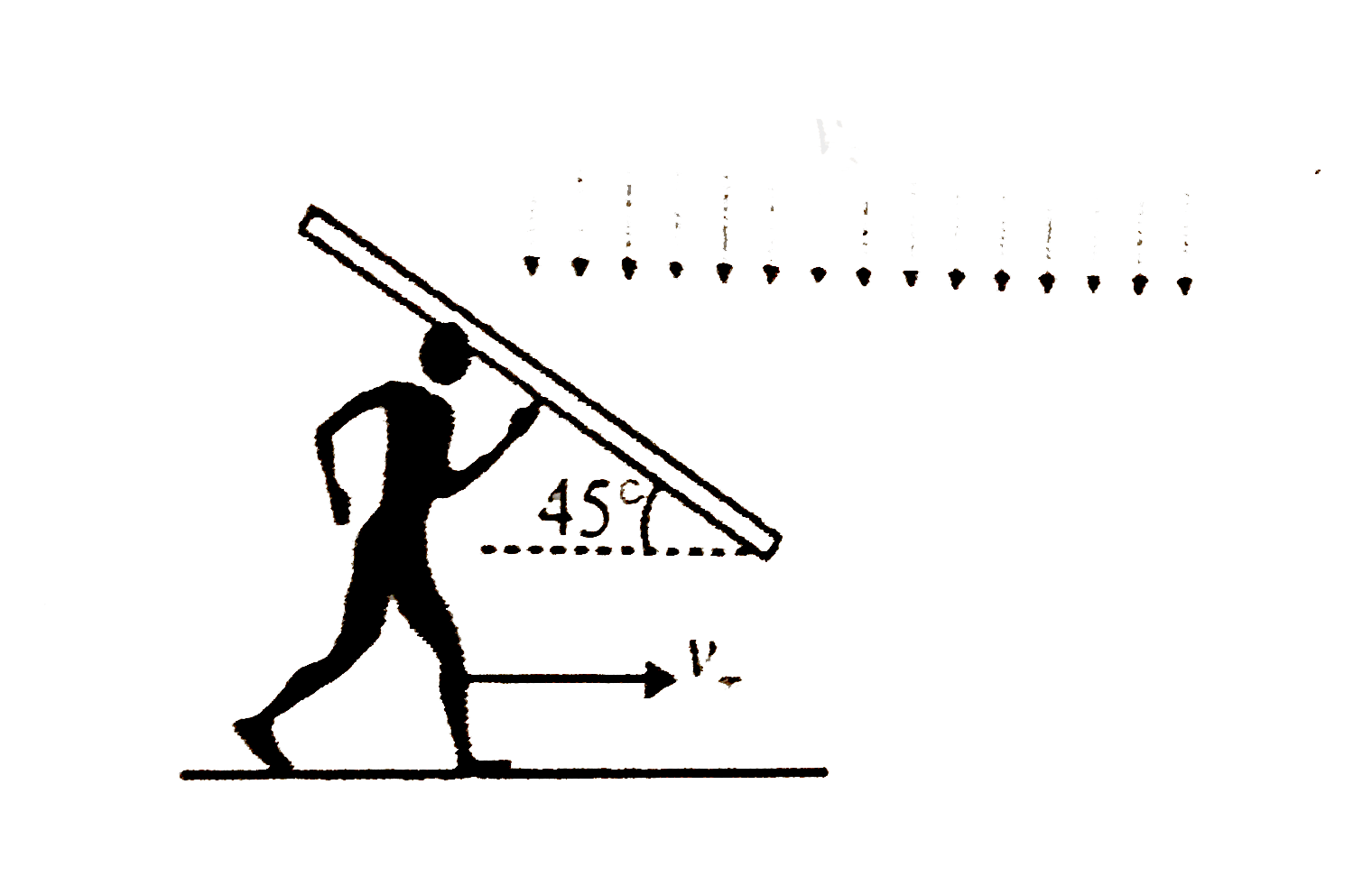 View Solution
View SolutionA rectangular tank of mass m0 and charge Q over it is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second, Mass of each drop is m. Find velocity of tank as function of time.
View SolutionA rectangular tank of mass m0 and charge Q is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second. Mass of each drop is m. Find velocity of tank as function of time.
View SolutionRain is falling vertically with velocity 10m /s and a man is moving with velocity 6ms−1. Find the angle at which the man should hold his umbrella to above getting wet.
View Solution

