A rectangular tank of mass and charge over it is placed over a smooth horizontal floor. A horizontal electric field exist in the region. Rain drops are falling vertically in the tank at the constant rate of drops per second, Mass of each drop is . Find velocity of tank as function of time.
To find the velocity of the tank as a function of time, we can follow these steps:
Step 1: Identify the forces acting on the tank
The forces acting on the tank are:
1. The electrostatic force Fe=QE acting horizontally due to the electric field.
2. The thrust force due to the rain drops falling into the tank, which can be expressed as Ft=mnv, where n is the rate of rain drops falling per second and m is the mass of each drop.
Step 2: Write the net force equation
The net force Fnet acting on the tank can be expressed as:
Fnet=Fe−Ft=QE−mnv
Step 3: Apply Newton's second law
According to Newton's second law, the net force is equal to the mass of the system times its acceleration:
Fnet=(m0+mn⋅t)dvdt
where m0 is the initial mass of the tank and mn⋅t is the mass added due to the rain drops over time t.
Step 4: Set up the differential equation
Equating the two expressions for the net force gives:
(m0+mn⋅t)dvdt=QE−mnv
Step 5: Rearranging the equation
Rearranging the equation, we have:
dvdt=QE−mnvm0+mn⋅t
Step 6: Separate variables and integrate
Separating variables, we get:
dvQE−mnv=dtm0+mn⋅t
Now we can integrate both sides. The left side with respect to v and the right side with respect to t.
Step 7: Perform the integration
Integrating the left side:
∫dvQE−mnv=−1mnln|QE−mnv|
Integrating the right side:
∫dtm0+mn⋅t=1mnln|m0+mn⋅t|
Step 8: Combine the results from integration
Setting the two integrals equal gives:
−1mnln|QE−mnv|=1mnln|m0+mn⋅t|+C
where C is the constant of integration.
Step 9: Solve for v
Exponentiating both sides and rearranging gives:
QE−mnv=K(m0+mn⋅t)−1
where K is a constant derived from C. Solving for v:
v=QEmn−Kmn(m0+mn⋅t)
Step 10: Determine the constant K
To find K, we can use the initial condition v(0)=0:
0=QEmn−Kmn(m0)
This allows us to solve for K.
Final Expression for Velocity
After substituting K back into the equation, we arrive at the final expression for the velocity of the tank as a function of time:
v(t)=QEmn(1−m0m0+mn⋅t)
The forces acting on the tank are:
1. The electrostatic force Fe=QE acting horizontally due to the electric field.
2. The thrust force due to the rain drops falling into the tank, which can be expressed as Ft=mnv, where n is the rate of rain drops falling per second and m is the mass of each drop.
The net force Fnet acting on the tank can be expressed as:
Fnet=Fe−Ft=QE−mnv
According to Newton's second law, the net force is equal to the mass of the system times its acceleration:
Fnet=(m0+mn⋅t)dvdt
where m0 is the initial mass of the tank and mn⋅t is the mass added due to the rain drops over time t.
Equating the two expressions for the net force gives:
(m0+mn⋅t)dvdt=QE−mnv
Rearranging the equation, we have:
dvdt=QE−mnvm0+mn⋅t
Separating variables, we get:
dvQE−mnv=dtm0+mn⋅t
Now we can integrate both sides. The left side with respect to v and the right side with respect to t.
Integrating the left side:
∫dvQE−mnv=−1mnln|QE−mnv|
Integrating the right side:
∫dtm0+mn⋅t=1mnln|m0+mn⋅t|
Setting the two integrals equal gives:
−1mnln|QE−mnv|=1mnln|m0+mn⋅t|+C
where C is the constant of integration.
Exponentiating both sides and rearranging gives:
QE−mnv=K(m0+mn⋅t)−1
where K is a constant derived from C. Solving for v:
v=QEmn−Kmn(m0+mn⋅t)
To find K, we can use the initial condition v(0)=0:
0=QEmn−Kmn(m0)
This allows us to solve for K.
After substituting K back into the equation, we arrive at the final expression for the velocity of the tank as a function of time:
v(t)=QEmn(1−m0m0+mn⋅t)
Similar Questions
A rectangular tank of mass m0 and charge Q is placed over a smooth horizontal floor. A horizontal electric field E exist in the region. Rain drops are falling vertically in the tank at the constant rate of n drops per second. Mass of each drop is m. Find velocity of tank as function of time.
View SolutionA ball of mass m having a charge q is released from rest in a region where a horizontal electric field E exists.
(a) Find the resultant force acting on the ball.
(b) Find the trajectory followed by the ball.
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
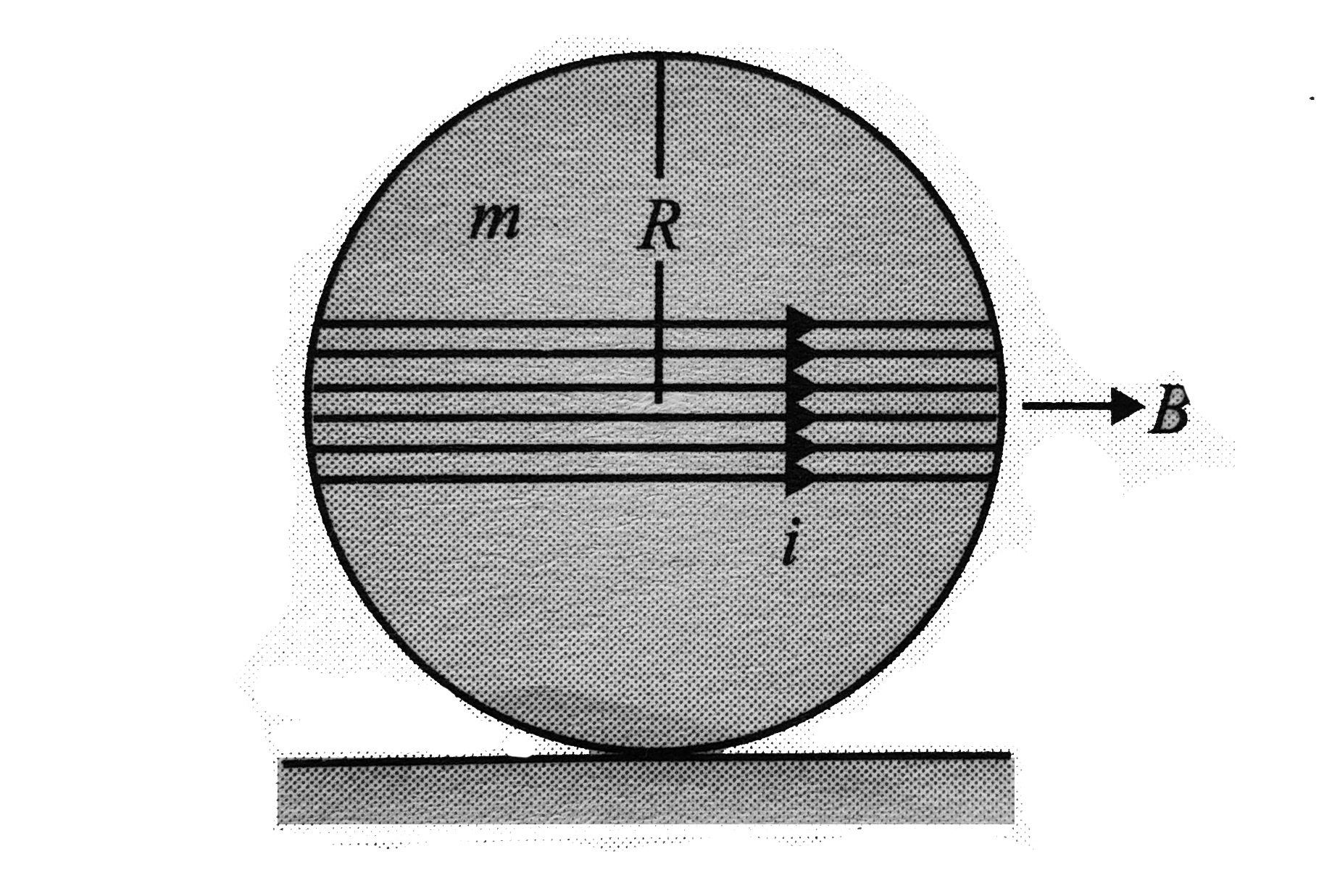
View SolutionA wire is wrapped N times over a solid sphere of mass m which is place on a smooth horizontal surface. A horizontal magnetic field of induction →B is present. Find the (a) torque (b) angular acceleration experienced by the sphere. Assume that the mass of the wire is negligible compared to the mass of the sphere.
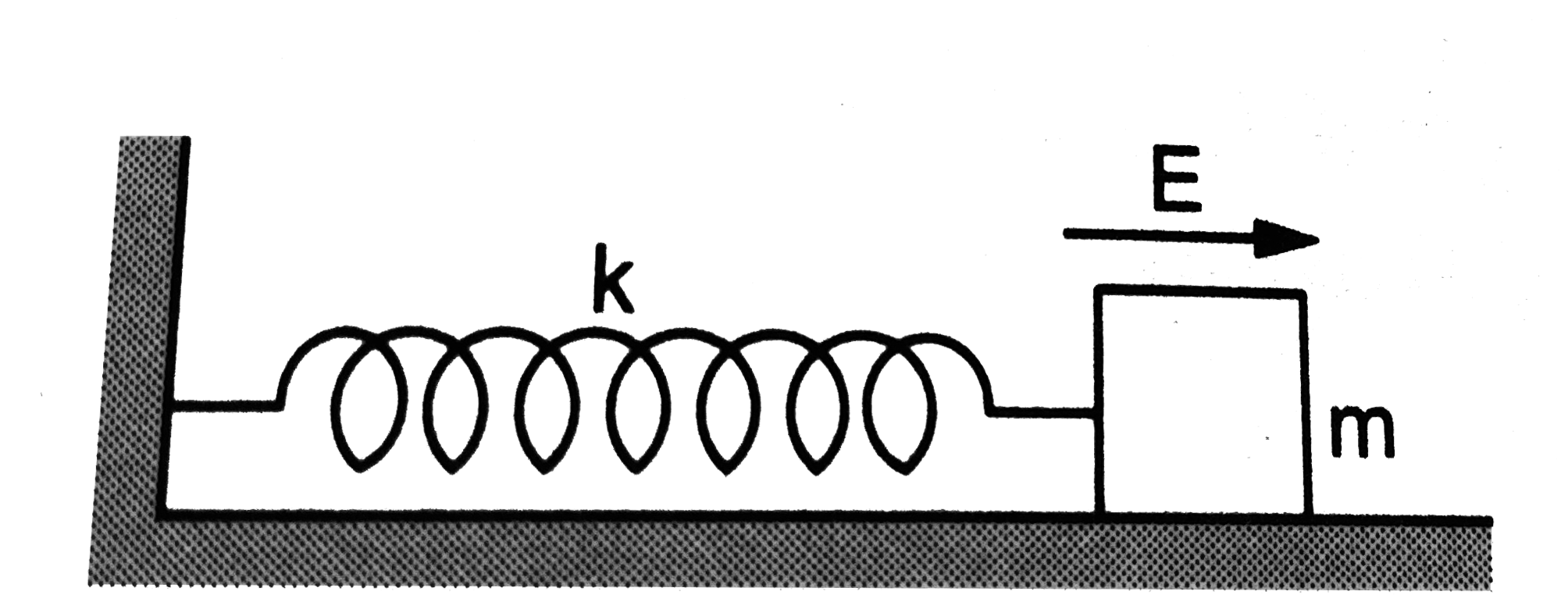
View SolutionA block of mass m having a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k as shown in figure(29.E1) . A horizontal electric field E parallel to the spring is switched on. Find the amplitude of the resulting SHM of the block.
View SolutionA small particle of mass m and charge Q is dropped in uniform horizontal magnetic field B. The maximum vertical displacement of particle is given by h=nm2g2Q2B2 . Find the value n.
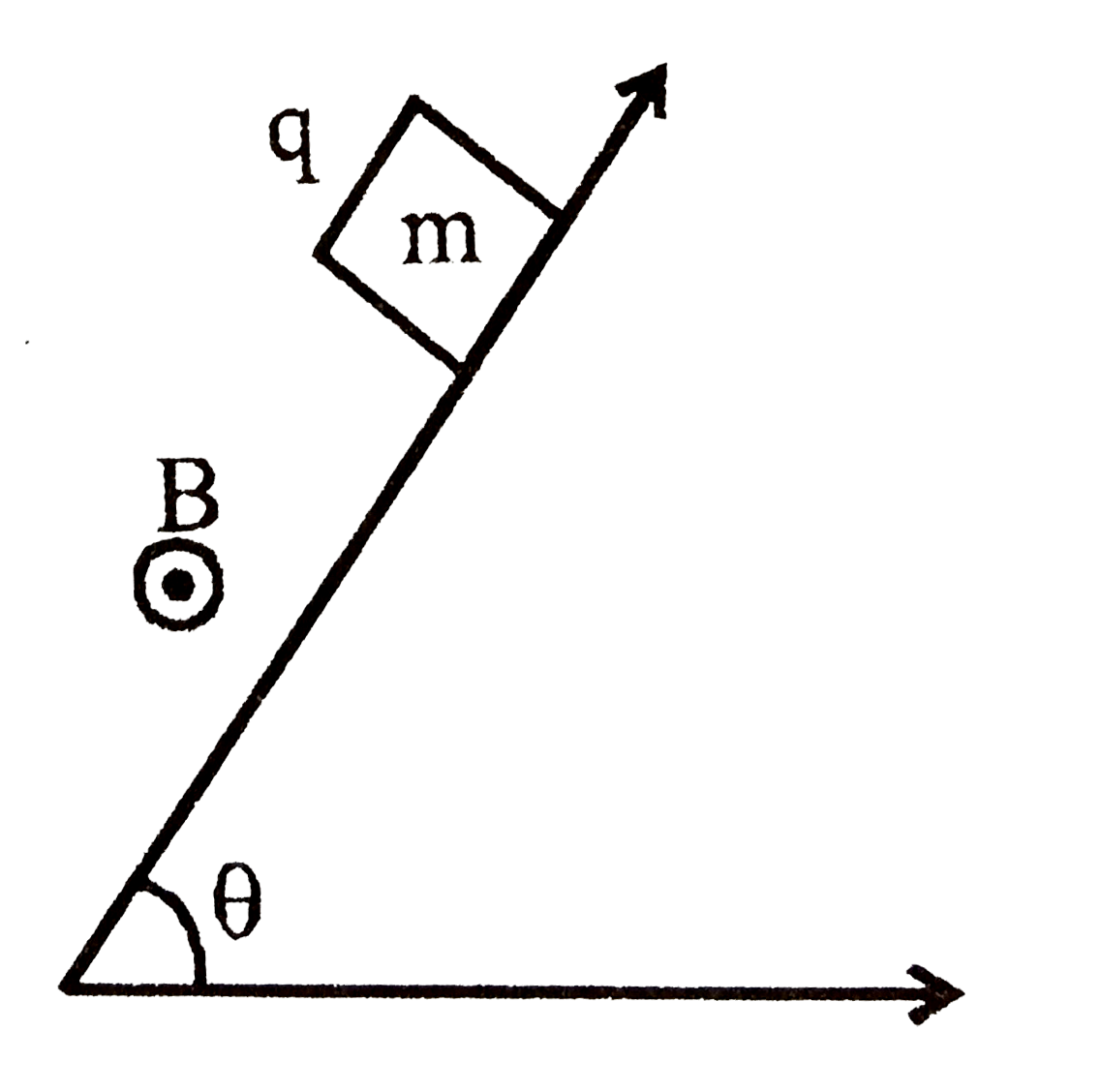
View SolutionA block of mass m & charge q is released on a long smooth inclined plane magnetic field B is constant, unifrom, horizontal and parallel to surface a shown Find the time from start when block loses contact with the surface
 .
.
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View Solution
