Prove that when the sides of a triagle are taken in order, it leads to zero resultant.
3 units
Topper's Solved these Questions
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -1)
13 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
Assertion: The minimum number of vectors of unequal magnitude required to produce zero resultant is three.
Reason: Three vectors of unequal magnitude which can be represented by the three sides of a triangle taken in order, produce zero resultant.
View SolutionIf →a, →b, →c be the vectors represented by the sides of a triangle, taken in order, then prove that →a+→b+→c=→0.
View SolutionIf →a, →b, →c represent the sides of a triangle taken in order, then write the value of →a+→b+→c
View SolutionIf →a,→band→c represents three sides of a triangle taken in order prove that
→a×→b=→b×→c=→c×→a
View SolutionThe quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if
View SolutionThe figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only, if
View SolutionIf A,B,C represents the three sides of an equilateral triangle taken in the same order then find the angle between i) A and B ii) B and C iii) A and C.
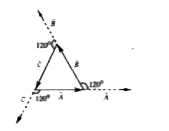
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionIf the mid-points of the sides of a quadrilateral are joined in order, prove that the area of the parallelogram, so formed will be half of the area of the given quadrilateral (figure).

View SolutionLet A1A2A3A4A5A6A1 be a regular hexagon. Write the x-components of the vectors representeed by the six sides taken in order. Use the fact that the resultant of these six vectors is zero, to prove that cos0+cosπ3+cos(2π)3+cos(4π)3+cos(5π)3=0 Use the known cosine values of verify the result.
 .
.
View Solution
