A 2kg block lying on smooth table which is connected by a body of mass 1 kg by a string which passes through a pulley. Take 1 kg mass hanging vertically. Find the acceleration of block & tension in string.
The correct Answer is:3.27m/s2;6.54N
To solve the problem, we need to analyze the forces acting on both the 2 kg block on the table and the 1 kg mass hanging vertically. We'll use Newton's second law of motion to find the acceleration and the tension in the string.
Step 1: Identify the masses and forces
- Mass of the block on the table (m1) = 2 kg
- Mass of the hanging block (m2) = 1 kg
- Acceleration due to gravity (g) = 9.8 m/s²
Step 2: Write the equations of motion
For the hanging mass (m2):
- The forces acting on it are the gravitational force (weight) downward and the tension (T) in the string upward.
- Using Newton's second law, we can write the equation:
m2g−T=m2a
Substituting the values:
1⋅9.8−T=1⋅a(1)
For the block on the table (m1):
- The only horizontal force acting on it is the tension (T) in the string.
- Again using Newton's second law, we write:
T=m1a
Substituting the values:
T=2a(2)
Step 3: Solve the equations
Now we have two equations:
1. 9.8−T=a
2. T=2a
Substituting equation (2) into equation (1):
9.8−2a=a
Combine like terms:
9.8=3a
Now, solve for a:
a=9.83≈3.27m/s2
Step 4: Find the tension in the string
Now that we have the acceleration, we can find the tension using equation (2):
T=2a=2⋅3.27≈6.54N
Final Results
- The acceleration of the block is approximately 3.27m/s2.
- The tension in the string is approximately 6.54N.
- Mass of the block on the table (m1) = 2 kg
- Mass of the hanging block (m2) = 1 kg
- Acceleration due to gravity (g) = 9.8 m/s²
For the hanging mass (m2):
- The forces acting on it are the gravitational force (weight) downward and the tension (T) in the string upward.
- Using Newton's second law, we can write the equation:
m2g−T=m2a
Substituting the values:
1⋅9.8−T=1⋅a(1)
- The only horizontal force acting on it is the tension (T) in the string.
- Again using Newton's second law, we write:
T=m1a
Substituting the values:
T=2a(2)
Now we have two equations:
1. 9.8−T=a
2. T=2a
9.8−2a=a
Combine like terms:
9.8=3a
Now, solve for a:
a=9.83≈3.27m/s2
Now that we have the acceleration, we can find the tension using equation (2):
T=2a=2⋅3.27≈6.54N
- The acceleration of the block is approximately 3.27m/s2.
- The tension in the string is approximately 6.54N.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - NUMERICAL EXERCISE ( LEVEL-2)
13 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWER
5 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
13 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
The strings are inextensible and light: the pulleys are smooth and light. Find the acceleration of each block and tensions in the strings.

View SolutionConsider the situation shown in the figure. The surface is smooth and the string and the pulley are light. Find the acceleration of each block and tension in the string.

View SolutionA block of mass M1=3kg on a smooth fixed inclined plane of angle 30∘ is connected by a cord over a small frictionless pulley to a second block mass 2kg hanging vertically. The tension in the cord and the acceleration of each block are ………............. and ...................... respectively.

View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View SolutionA block of mass m1=2kg on a smooth inclined planeat angle 30∘ is connected to a second block of mass m2=3kg by a cord passing over a frictionless pulley as shown in figure. The acceleration of each block is - (Assume g=10m/sec2 )
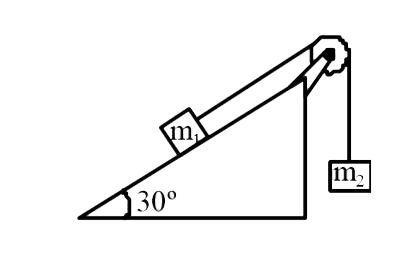
View SolutionIn the above example, if two blocks have masses 1kg and 2kg respectively then find their acceleration and tension in different string.
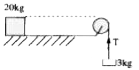
View SolutionA body of mass 20kg is moving on a rough horizontal plane. A block of mass 3kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The tension in the string is 27 N. The coefficient of kinetic friction between the heavier mass and the surface is (g = 10m/s2)
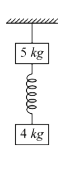
View SolutionTwo block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View Solution
