Two blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
6.54m/s2,26N
2.6m/s2,6.54N
6.54m/s2,13N
13m/s2,26N
The correct Answer is:C
To solve the problem, we will analyze the forces acting on the two blocks and apply Newton's second law of motion.
Step 1: Identify the masses and forces acting on each block.
- Mass of block on the table, m1=2kg
- Mass of hanging block, m2=4kg
- The force acting on the hanging block due to gravity is Fg2=m2⋅g=4⋅9.8=39.2N (where g≈9.8m/s2).
- The tension in the string is T.
Hint: Remember that the tension acts upwards on the hanging block and horizontally on the block on the table.
---
Step 2: Write the equations of motion for both blocks.
For the block on the table (2 kg):
T=m1⋅a(1)
For the hanging block (4 kg):
m2⋅g−T=m2⋅a(2)
Hint: Use Newton's second law, F=m⋅a, for both blocks.
---
Step 3: Substitute the values into the equations.
From equation (1):
T=2a(3)
Substituting equation (3) into equation (2):
4g−2a=4a
Hint: Substitute T from equation (1) into the second equation to eliminate T.
---
Step 4: Solve for acceleration a.
Rearranging the equation:
4g=4a+2a
4g=6a
a=4g6=2g3
Substituting g=9.8m/s2:
a=2⋅9.83≈6.53m/s2
Hint: Make sure to calculate g accurately and simplify the fraction correctly.
---
Step 5: Find the tension T in the string.
Using equation (3):
T=2a=2⋅(2g3)=4g3
Substituting g=9.8m/s2:
T=4⋅9.83≈13.07N
Hint: Use the value of a you found to calculate T.
---
Final Answers:
(i) The acceleration of the system is approximately 6.53m/s2.
(ii) The tension in the string is approximately 13.07N.
- Mass of hanging block, m2=4kg
- The force acting on the hanging block due to gravity is Fg2=m2⋅g=4⋅9.8=39.2N (where g≈9.8m/s2).
- The tension in the string is T.
T=m1⋅a(1)
m2⋅g−T=m2⋅a(2)
T=2a(3)
4g−2a=4a
4g=4a+2a
4g=6a
a=4g6=2g3
a=2⋅9.83≈6.53m/s2
T=2a=2⋅(2g3)=4g3
T=4⋅9.83≈13.07N
(i) The acceleration of the system is approximately 6.53m/s2.
Similar Questions
Two bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionThree blocks of masses 3 kg, 6 kg and 1 kg are connected by a string passing over two smooth pulleys attached at the two ends of the horizontal surface. If the co-efficient of friction between the block and the surface is 0.6, the frictional force acting on the block of mass 6 kg is
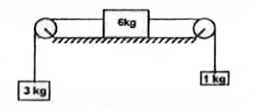
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
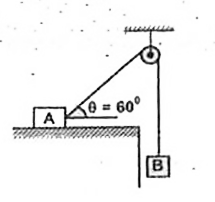
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
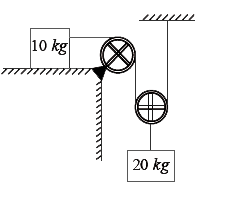
View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View SolutionTwo unequal masses are connected by a very light string over a clamped light smooth pulley. Find the acceleration of the system and the tension in the string.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View Solution
