A 1000 kg lift is supported by a cable that can support 2000 kg. The shortest distance in which the lift can be stopped when it is descending with a speed of 2.5m/s is (g=10m/s2)
516m
532m
1m
2m
The correct Answer is:1
To solve the problem, we need to determine the shortest distance in which a 1000 kg lift can be stopped when it is descending with a speed of 2.5 m/s. We will use the concepts of forces, acceleration, and equations of motion.
1. Identify the Forces Acting on the Lift:
- The weight of the lift (W) is given by:
W=mg=1000kg×10m/s2=10000N
- The maximum tension (T) the cable can support is:
T=2000kg×10m/s2=20000N
2. Determine the Net Force Acting on the Lift:
- When the lift is descending and we want to stop it, the tension in the cable must overcome its weight. The net force (F_net) acting on the lift can be expressed as:
Fnet=T−W=20000N−10000N=10000N
3. Calculate the Acceleration of the Lift:
- Using Newton's second law, F=ma, we can find the acceleration (a):
Fnet=ma⟹10000N=1000kg×a
a=10000N1000kg=10m/s2
4. Use the Equation of Motion to Find the Stopping Distance:
- We will use the equation:
v2=u2+2as
- Here, v=0m/s (final velocity when stopped), u=2.5m/s (initial velocity), and a=−10m/s2 (deceleration, negative because it is stopping).
- Rearranging the equation gives:
0=(2.5)2+2(−10)s
0=6.25−20s
20s=6.25⟹s=6.2520=0.3125m
5. Convert to Fraction:
- The distance can also be expressed as:
s=516m
Final Answer:
The shortest distance in which the lift can be stopped is 516m.
---
- The weight of the lift (W) is given by:
W=mg=1000kg×10m/s2=10000N
- The maximum tension (T) the cable can support is:
T=2000kg×10m/s2=20000N
- When the lift is descending and we want to stop it, the tension in the cable must overcome its weight. The net force (F_net) acting on the lift can be expressed as:
Fnet=T−W=20000N−10000N=10000N
- Using Newton's second law, F=ma, we can find the acceleration (a):
Fnet=ma⟹10000N=1000kg×a
a=10000N1000kg=10m/s2
- We will use the equation:
v2=u2+2as
- Here, v=0m/s (final velocity when stopped), u=2.5m/s (initial velocity), and a=−10m/s2 (deceleration, negative because it is stopping).
- Rearranging the equation gives:
0=(2.5)2+2(−10)s
0=6.25−20s
20s=6.25⟹s=6.2520=0.3125m
- The distance can also be expressed as:
s=516m
The shortest distance in which the lift can be stopped is 516m.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A lift of mass m is supported by a cable that can with stand a force of 3mg. Find the shortest distance in which the lift can be stopped when it is descending with a speed of g/4.
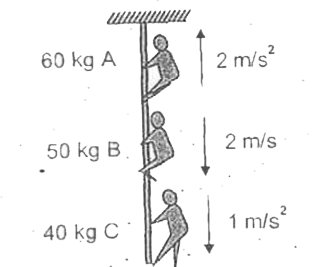
View SolutionTension in the rope at the rigid support is (g=10m/s2)
View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
The lift is descending with a constant velocity of 2 m/s.
View SolutionA man of mass 60 kg records his weight on a weighing machine placed inside a lift . The ratio of the weights of the man recorded when the lift is ascending up with a uniform speed of 2 m/s to when it is descending down with a uniform speed of 4 m/s will be
View SolutionThe mass of a lift is 2000kg . When the tensioon in the supporting cable is 28000N , then its acceleration is.
View SolutionA lift a mass 1200kg is raised from rest by a cable with a tension 1350kgf . After same time the tension drops to 1000kgf and the lift comes to rest at a height of 25m above its intial point (1kg−f=9.8N)
What is the greatest speed of lift?
View SolutionThe average power of the pump which lifts 20kg of water per second from a well 10m deep and projects it with a velocity 10m/s is (g=10m/s2)
View SolutionThe average power of the pump which lifts 20kg of water per second from a well 10m deep and projects it with a velocity 10m/s is (g=10m/s2)
View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
The lift is ascending with an acceleration of 2m/s2.
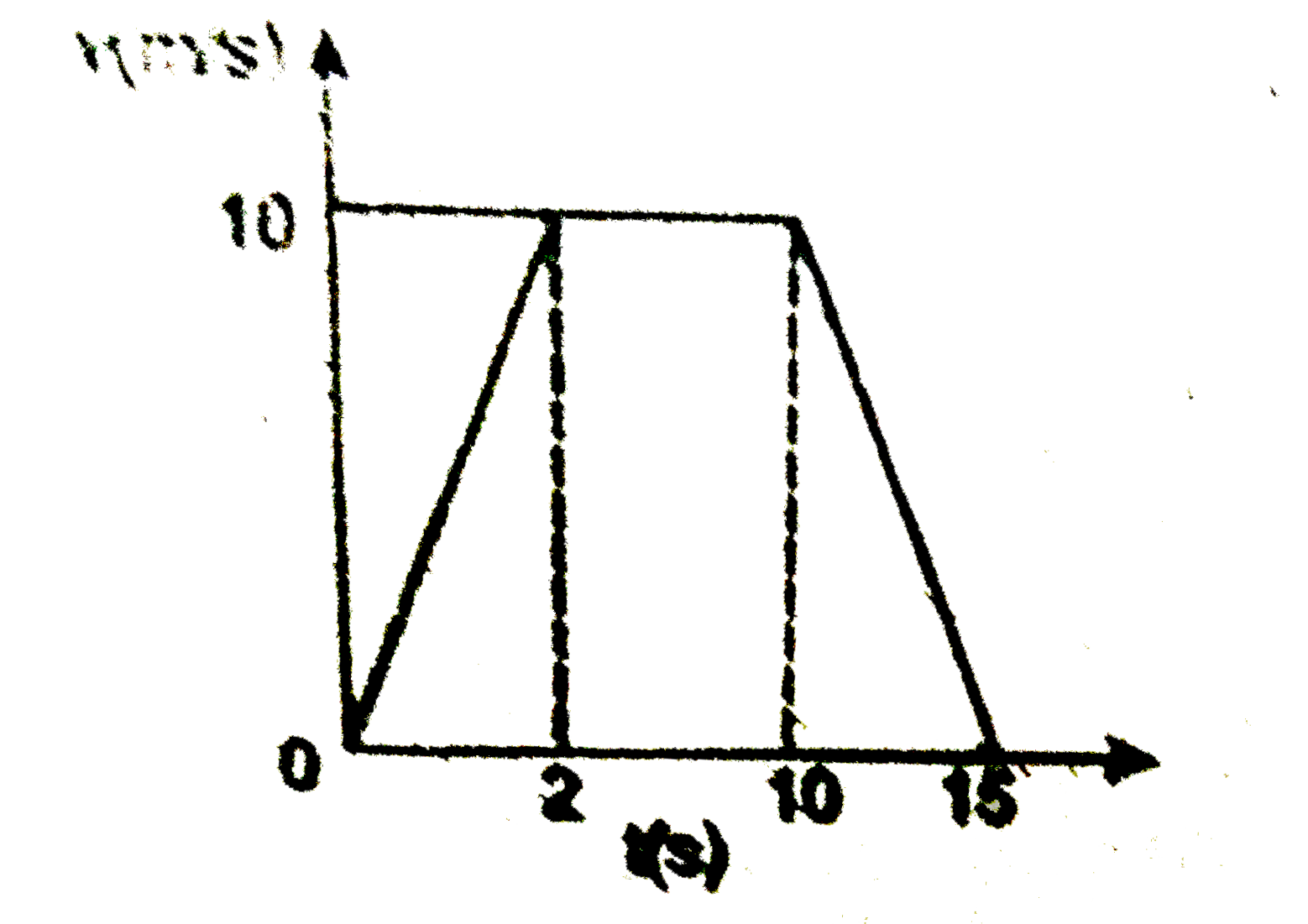
View SolutionA lift of mass 1000 kg is going up. The variation in the speed of lift is shown in figure. Then the minimum tension in the rope will be (g=10m/s2)
View Solution
