A piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
The correct Answer is:x=a2kg
To solve the problem, we need to analyze the forces acting on the bead when the wire is accelerated. Let's break it down step by step.
Step 1: Understand the Setup
The wire is shaped like a parabola given by the equation y=kx2. The bead can slide along this wire without friction. Initially, when the wire is at rest, the bead is at the lowest point, which is at the origin (0,0).
Step 2: Analyze the Forces Acting on the Bead
When the wire is accelerated with a constant acceleration a in the x-direction, the bead experiences two forces:
1. The gravitational force acting downwards: →Fg=m→g
2. A pseudo force acting in the opposite direction of the acceleration due to the wire's motion: →Fp=−m→a
Step 3: Break Down the Forces
At the new equilibrium position, the normal force →N acting on the bead can be resolved into two components:
- Ncos(θ) balancing the gravitational force mg
- Nsin(θ) balancing the pseudo force ma
Step 4: Set Up the Equations
From the balance of forces, we have:
1. Ncos(θ)=mg (1)
2. Nsin(θ)=ma (2)
Step 5: Divide the Equations
Dividing equation (2) by equation (1):
Nsin(θ)Ncos(θ)=mamg
This simplifies to:
tan(θ)=ag
Step 6: Relate the Angle to the Parabola
The slope of the parabola at any point x is given by the derivative of y with respect to x:
dydx=d(kx2)dx=2kx
Thus, at the new equilibrium position, we have:
tan(θ)=2kx
Step 7: Equate the Two Expressions for tan(θ)
From the previous steps, we have:
2kx=ag
Solving for x:
x=a2kg
Conclusion
The x-coordinate where the bead can stay at rest with respect to the wire when it is accelerated is:
x=a2kg
The wire is shaped like a parabola given by the equation y=kx2. The bead can slide along this wire without friction. Initially, when the wire is at rest, the bead is at the lowest point, which is at the origin (0,0).
When the wire is accelerated with a constant acceleration a in the x-direction, the bead experiences two forces:
1. The gravitational force acting downwards: →Fg=m→g
2. A pseudo force acting in the opposite direction of the acceleration due to the wire's motion: →Fp=−m→a
At the new equilibrium position, the normal force →N acting on the bead can be resolved into two components:
- Ncos(θ) balancing the gravitational force mg
- Nsin(θ) balancing the pseudo force ma
From the balance of forces, we have:
1. Ncos(θ)=mg (1)
2. Nsin(θ)=ma (2)
Dividing equation (2) by equation (1):
Nsin(θ)Ncos(θ)=mamg
This simplifies to:
tan(θ)=ag
The slope of the parabola at any point x is given by the derivative of y with respect to x:
dydx=d(kx2)dx=2kx
Thus, at the new equilibrium position, we have:
tan(θ)=2kx
From the previous steps, we have:
2kx=ag
Solving for x:
x=a2kg
The x-coordinate where the bead can stay at rest with respect to the wire when it is accelerated is:
x=a2kg
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Problem
162 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application
6 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - NUMERICAL EXERCISE ( LEVEL-2)
13 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View Solution
Knowledge Check
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
Aa/gkBa/2gkC2a/gkDa/4gk
A straight wire carrying current is parallel to the y-axis as shown in Fig. The
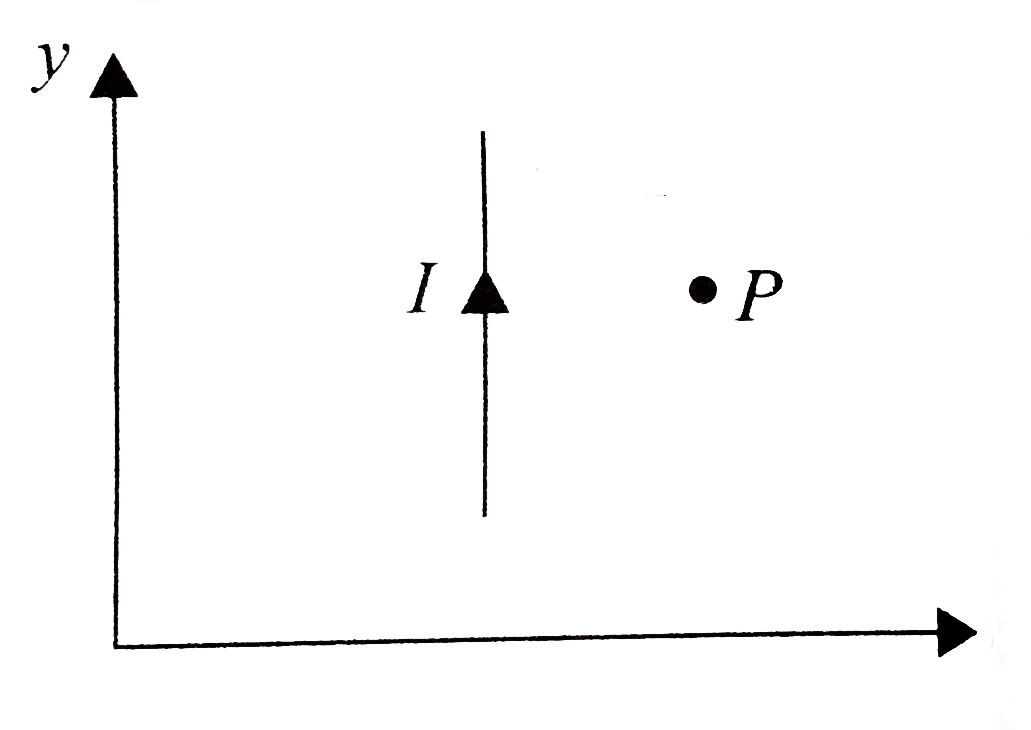
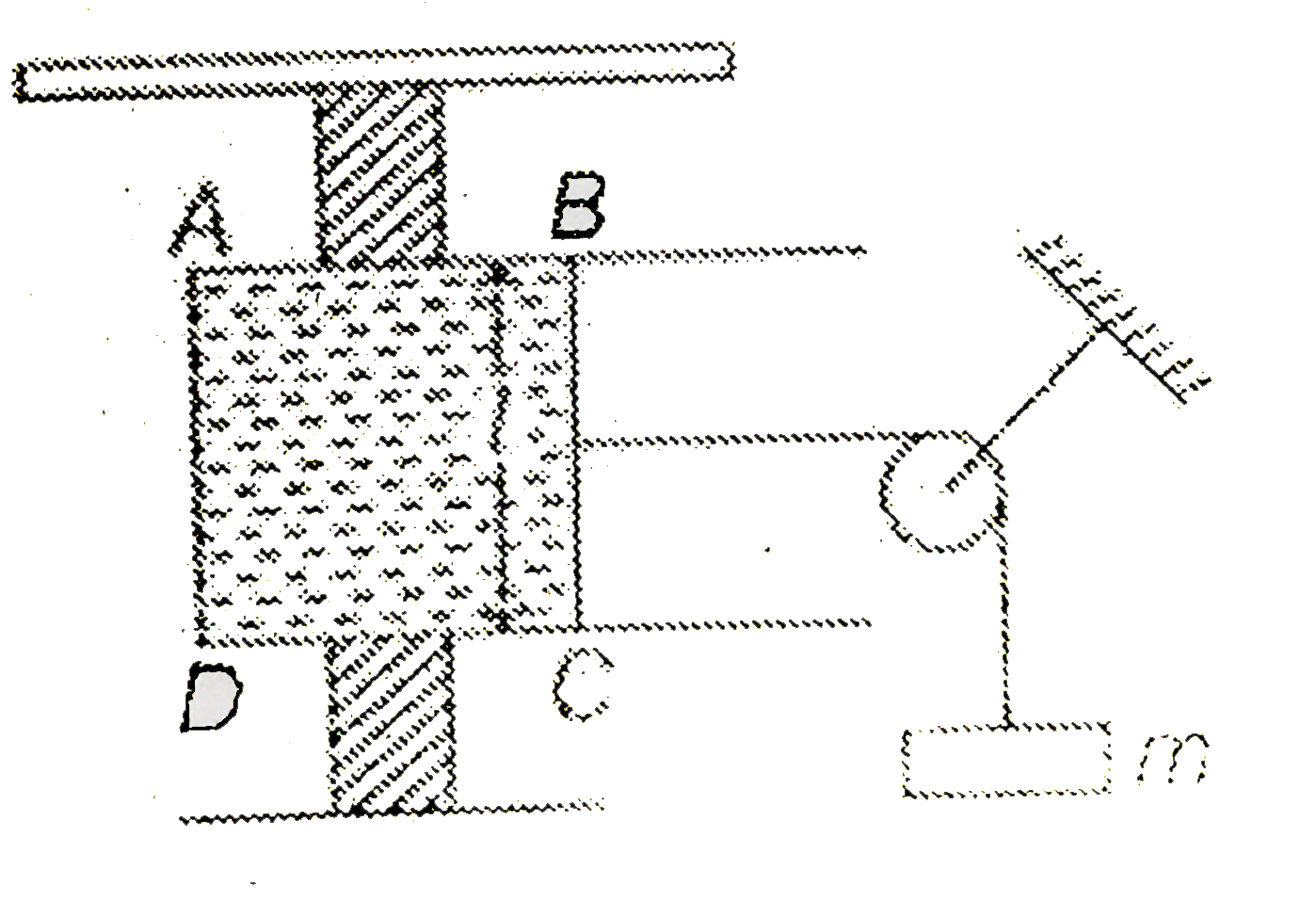
View SolutionA wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
View SolutionA bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
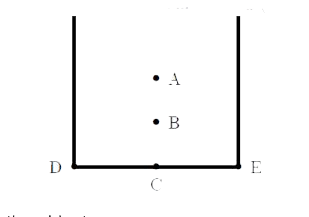
View SolutionA thick uniform wire is bent into the shape of the letter “U” as shown. Which point indicates the location of the center of mass of this wire?
View SolutionA uniform wire of length l is bent into the shape of 'V' as shown. The distance of its centre of mass from the vertex A is :-

View SolutionThe resistance of a wire R Ω . The wire is stretched to double its length keeping volume constant. Now, the resistance of the wire will become
View SolutionA piece of land is in the shape of an equilateral triangle. Its boundary has to be fenced with barbed wire. What is the length of the barbed wire required?
View Solution
