A bead of mass m is fitted on a rod and can move on it without friction. Initially the bead is at the middle of the rod moves transitionally in the vertical plane with an accleration a0 in direction forming angle α with the rod as shown. The acceleration of bead with respect to rod is:
z
To solve the problem, we need to analyze the forces acting on the bead and determine its acceleration with respect to the rod. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a bead of mass m that can move along a rod without friction. The rod is oriented at an angle α with respect to the vertical. The bead is initially at the midpoint of the rod and is subjected to a translational acceleration a0 at an angle α with the rod.
Step 2: Break Down the Acceleration
The acceleration a0 can be broken down into two components:
- Parallel to the rod: a0,∥=a0cos(α)
- Perpendicular to the rod: a_{0,\perpendicular} = a_0 \sin(\alpha)
Step 3: Analyze the Forces
The forces acting on the bead include:
1. The gravitational force mg acting downwards.
2. The component of the gravitational force acting along the rod, which can be expressed as mgsin(α).
3. The component of the translational acceleration acting along the rod, which is a0cos(α).
Step 4: Apply Newton's Second Law
Using Newton's second law, we can express the net acceleration of the bead along the rod. The net force acting on the bead along the direction of the rod is given by:
Fnet=mgsin(α)−ma0cos(α)
According to Newton's second law:
Fnet=manet
Thus, we can write:
mgsin(α)−ma0cos(α)=manet
Dividing through by m:
gsin(α)−a0cos(α)=anet
Step 5: Conclusion
The acceleration of the bead with respect to the rod is:
anet=gsin(α)−a0cos(α)
We have a bead of mass m that can move along a rod without friction. The rod is oriented at an angle α with respect to the vertical. The bead is initially at the midpoint of the rod and is subjected to a translational acceleration a0 at an angle α with the rod.
The acceleration a0 can be broken down into two components:
- Parallel to the rod: a0,∥=a0cos(α)
- Perpendicular to the rod: a_{0,\perpendicular} = a_0 \sin(\alpha)
The forces acting on the bead include:
1. The gravitational force mg acting downwards.
2. The component of the gravitational force acting along the rod, which can be expressed as mgsin(α).
3. The component of the translational acceleration acting along the rod, which is a0cos(α).
Using Newton's second law, we can express the net acceleration of the bead along the rod. The net force acting on the bead along the direction of the rod is given by:
Fnet=mgsin(α)−ma0cos(α)
According to Newton's second law:
Fnet=manet
Thus, we can write:
mgsin(α)−ma0cos(α)=manet
Dividing through by m:
gsin(α)−a0cos(α)=anet
The acceleration of the bead with respect to the rod is:
anet=gsin(α)−a0cos(α)
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.111videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
A ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
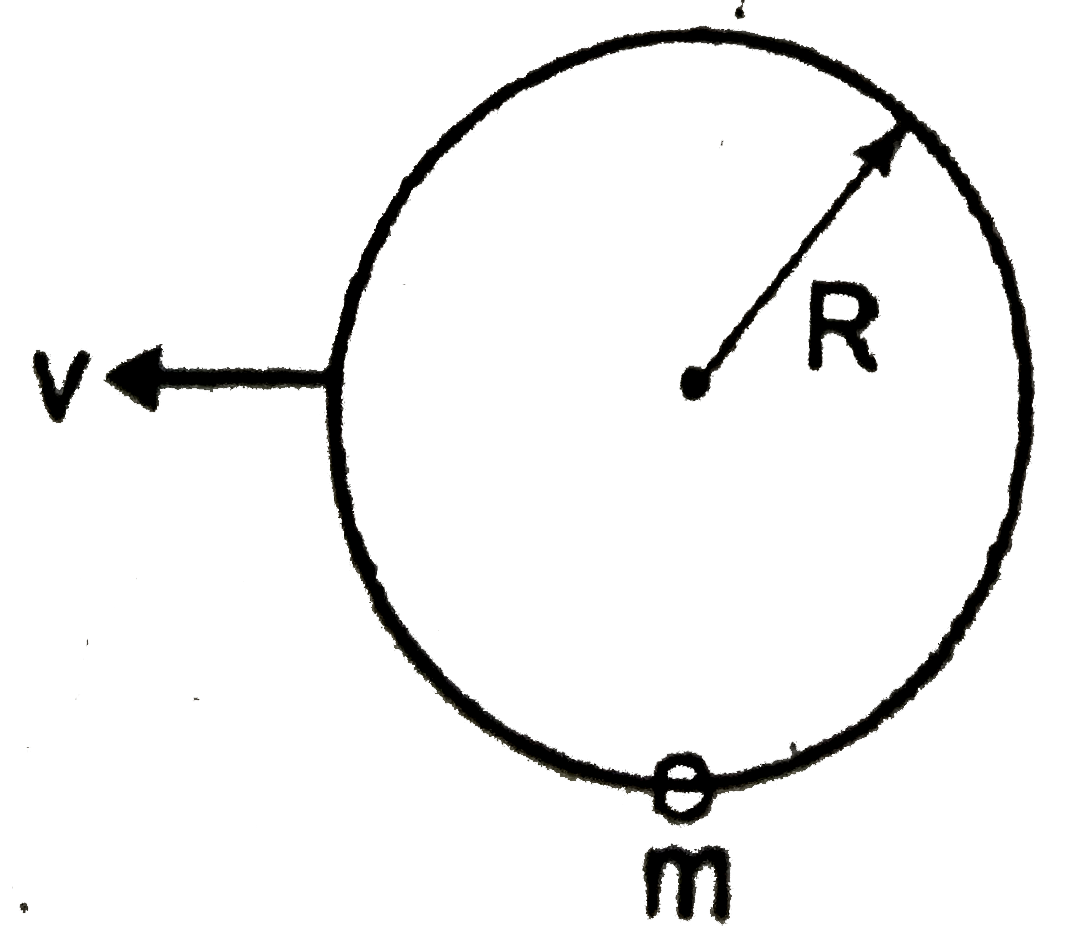 View Solution
View SolutionA ring of radius R lies in vertical plane. A bead of mass 'm' can move along the ring without friction. Initially the bead is at rest the bottom most point on ring. The minimum horizontal speed v with which the ring must be pulled such that the bead completes the vertical circle.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
Aa/gkBa/2gkC2a/gkDa/4gk
A piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionThe rod of length l and mass m lies on a smooth floor. A ball of mass m moving horizotally with a speed u0 striked one end of rod and stick to it. After the collision, the point on the rod that moves translationally ( without any rotation) in the previous direction of motion of the ball.

A. Is the centre of C of the rod.
B. Is the left end A of the rod.
C. Lies at a distance l/4 to the left of point C
D. Lies at a distance l/4 to the right of point C.View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
 View Solution
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
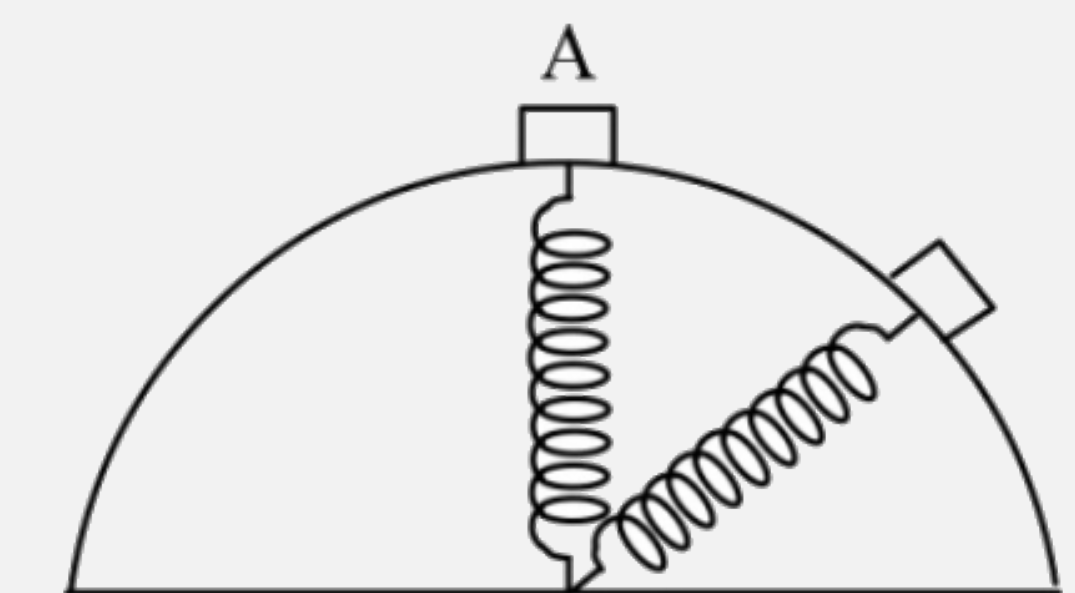 View Solution
View SolutionTwo balls of mass m and 4m are connected by a rod of length L. The mass of the rod is small and can be treated as zero . The size of the balls also can of the neglected . We also assume the centre of the rod is hinged ,but the rod can rotate about its centre in the vertical plane without friction . What is the gravity - induced angular acceleration of the rod when the angle between the rod and the vertical is θ as shown ?
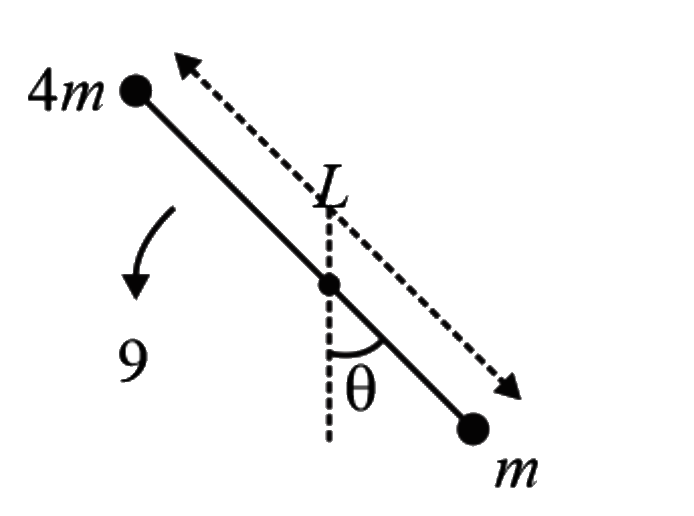 View Solution
View Solution

