A particle is projectedfrom the origin in X-Yplane. Acceleration of particle in Y direction is a. If equation of path of the particle isy = ax−bx2, then find initial velocity of the particle.
y=ax−bx2 y=xtanθ=αx22ucos2θ
tanθ=aandα2ucos2θ=bu=√α(1+a2)2b
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
A particle is projected from the origin in X-Y plane. Acceleration of particle in Y direction is a. If equation of path of the particle is y=ax−bx2, then find initial velocity of the particle.
View SolutionProjectile motion is a combination of two one-dimensional motion: one in horizontal and other in vertical direction. Motion in 2D means in a plane. Necessary condition for 2D motion is that the velocity vector is coplanar to the acceleration vector. In case of projectile motion, the angle between velocity and acceleration will be 0∘<θ<180∘. During the projectile motion, the horizontal component of velocity ramains unchanged but the vertical component of velocity is time dependent. Now answer the following questions:
A particle is projected from the origin in the x-y plane. The acceleration of particle in negative y-direction is α. If equation of path of the particle is y=ax−bx2, then initial velocity of the particle is
View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionAcceleration of a particle at any time t is →a=(2tˆi+3t2ˆj)m/s2.If initially particle is at rest, find the velocity of the particle at time t=2s
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:
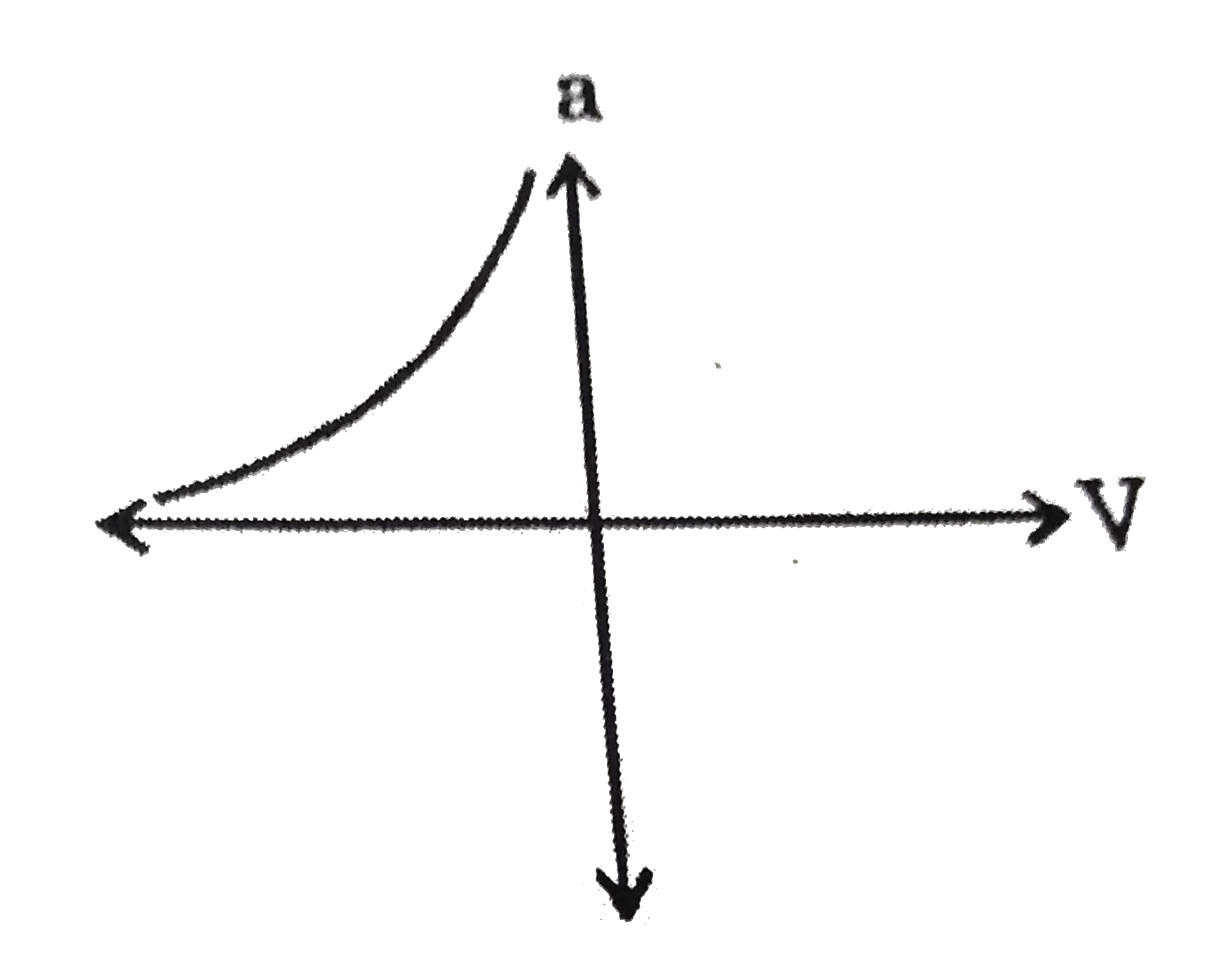
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View SolutionThe velocity time relation of a particle is given by v =(3t2−2t−1)m/s Calculate the position and acceleration of the particle when velocity of the particle is zero . Given the initial position of the particle is 5m .
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
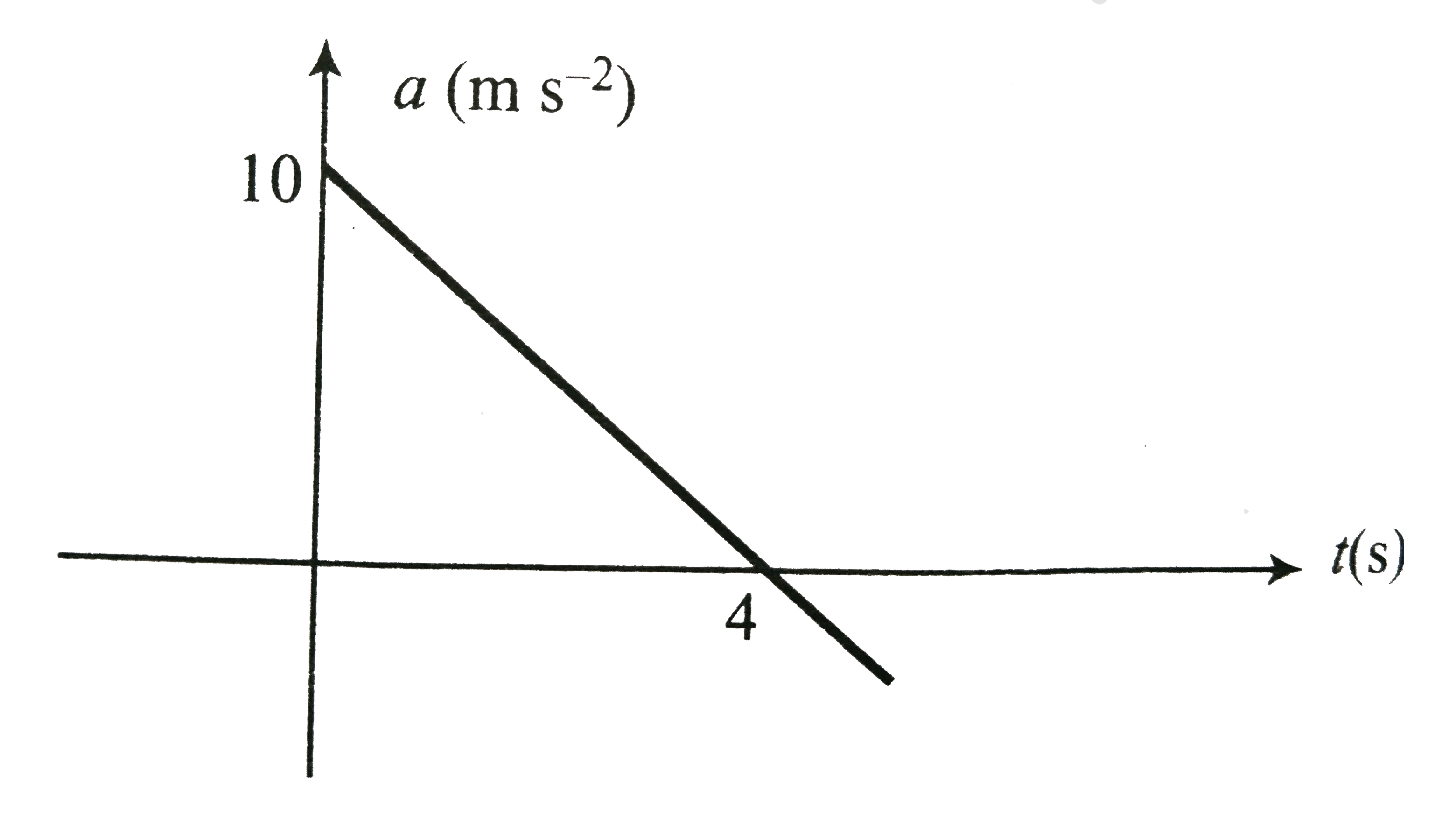 .
.
View SolutionThe acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
 .
.
View Solution
