(A) : A rocket works on the principle of conservation of linear momentum.
(r) : When there is no external force on a system of two bodies the rate of change in momenta of two bodies are equal and opposite
Both (A) and (R) are true and (R) is the correct explanation of (A)
Both (A) and (R) are true and (R) is not the
(A) is true but ( R) is false
Both (A) and (R ) are false
The correct Answer is:A
To solve the question, we need to analyze the two statements provided:
Statement A: A rocket works on the principle of conservation of linear momentum.
Statement R: When there is no external force on a system of two bodies, the rate of change of momentum of the two bodies is equal and opposite.
Step 1: Understanding Statement R
- According to Newton's second law, the net force acting on a system is equal to the rate of change of momentum. If there is no external force acting on the system, the net force is zero.
- Mathematically, this can be expressed as:
Fnet=0⟹dP1dt+dP2dt=0
- This implies that:
dP1dt=−dP2dt
- This means that the rate of change of momentum of the first body is equal in magnitude but opposite in direction to that of the second body. Thus, Statement R is true.
Step 2: Understanding Statement A
- A rocket operates based on the principle of conservation of linear momentum. When a rocket expels gas (fuel) downwards, it experiences an equal and opposite reaction that propels it upwards.
- Initially, the momentum of the system (rocket + fuel) is conserved. When the fuel is expelled, the momentum of the rocket increases in the upward direction while the momentum of the expelled fuel is in the downward direction.
- Mathematically, if the mass of the rocket is M1 and its velocity is V1, and the mass of the expelled fuel is M2 with velocity V2, the conservation of momentum can be expressed as:
M1V1+M2(−V2)=0
- This shows that the momentum before and after the fuel is expelled remains constant, confirming that Statement A is also true.
Step 3: Relationship Between A and R
- Statement R provides a fundamental principle that explains why Statement A is true. The conservation of momentum in the rocket's operation is a direct application of the principle stated in R.
- Therefore, both statements are true, and R is the correct explanation of A.
Conclusion
Both statements A and R are true, and R is the correct explanation of A.
---
- According to Newton's second law, the net force acting on a system is equal to the rate of change of momentum. If there is no external force acting on the system, the net force is zero.
- Mathematically, this can be expressed as:
Fnet=0⟹dP1dt+dP2dt=0
- This implies that:
dP1dt=−dP2dt
- This means that the rate of change of momentum of the first body is equal in magnitude but opposite in direction to that of the second body. Thus, Statement R is true.
- A rocket operates based on the principle of conservation of linear momentum. When a rocket expels gas (fuel) downwards, it experiences an equal and opposite reaction that propels it upwards.
- Initially, the momentum of the system (rocket + fuel) is conserved. When the fuel is expelled, the momentum of the rocket increases in the upward direction while the momentum of the expelled fuel is in the downward direction.
- Mathematically, if the mass of the rocket is M1 and its velocity is V1, and the mass of the expelled fuel is M2 with velocity V2, the conservation of momentum can be expressed as:
M1V1+M2(−V2)=0
- This shows that the momentum before and after the fuel is expelled remains constant, confirming that Statement A is also true.
- Statement R provides a fundamental principle that explains why Statement A is true. The conservation of momentum in the rocket's operation is a direct application of the principle stated in R.
- Therefore, both statements are true, and R is the correct explanation of A.
Both statements A and R are true, and R is the correct explanation of A.
Similar Questions
The work done by the external forces on a system equals the change in
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View SolutionThe work done by all the forces (external and internal) on a system equals the change in
View SolutionThe work done by all the forces (external and internal) on a system equals the change in
View SolutionWhen a conservation force does positive work on a body, then the
View SolutionA force-time graph for the motion of a body is shown in fig. change in linear momentum between 0 and 8 s is:-
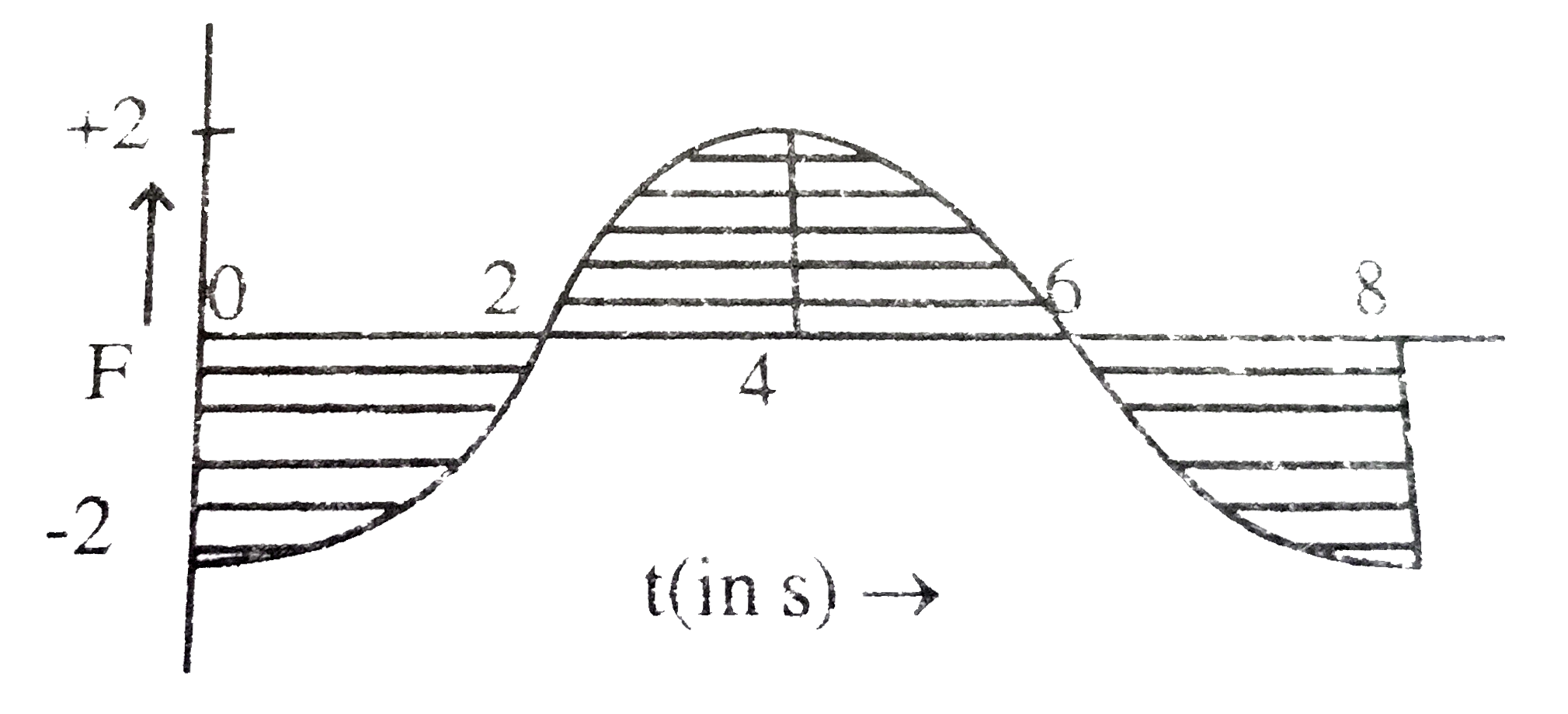
View SolutionA force-time graph for the motion of a body is shown in fig. Change in linear momentum between 0 and 8s is :
View SolutionUnderline the correct alterntaive:
a) when a conservative force does positivie work on a body, the potential energy of the body increase/decreases/remains unaltered.
work done by a body against friction always results in a loss of its kinetic /potential energy.
c) The rate of change of total momentum of a many-particle system is proportional to the external force/ sum of the internal forces on the system.
d) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy/total linear momentum/total enregy of the system of two bodies.
View SolutionSuppose we define a quantity Linear Momentum as linear momentum =mass x speed.
The linear momentum of a system of particles is the sum of linear momentum of the individual particles. Can we state a principle of conservation of linear momentum as linear momentum of a system remains constant if no external force acts on it?
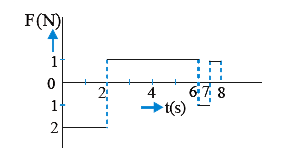
View SolutionA force-time graph for the motion of a body is shown in figure. Change in linear momentum between 0 and 8 s is:

View Solution
