A mass 'M' is suspended by a rope from a rigid support. It is pulled horizontally with a force F. If the rope makes an angle ' θ' with vertical in equilibrium, then the tention in the string is
Fsinθ
Fsinθ
Fcosθ
Fcosθ
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the mass M suspended by the rope and how they relate to the tension in the rope when it is pulled horizontally with a force F.
1. Draw the Free Body Diagram (FBD):
- Start by drawing the mass M suspended from a rigid support by a rope.
- Indicate the angle θ that the rope makes with the vertical.
- Mark the weight of the mass acting downward as W=Mg (where g is the acceleration due to gravity).
- Indicate the horizontal force F acting on the mass.
2. Identify Forces:
- The tension T in the rope acts along the rope at an angle θ from the vertical.
- The weight W acts downward.
- The horizontal force F acts to the right.
3. Resolve the Tension into Components:
- The tension T can be resolved into two components:
- Vertical component: Tcos(θ) (acting upward)
- Horizontal component: Tsin(θ) (acting horizontally)
4. Set Up Equilibrium Conditions:
- Since the mass is in equilibrium, the sum of the forces in both the vertical and horizontal directions must be zero.
- For vertical forces:
Tcos(θ)=Mg(1)
- For horizontal forces:
Tsin(θ)=F(2)
5. Solve for Tension T:
- From equation (2), we can express T in terms of F and θ:
T=Fsin(θ)(3)
- From equation (1), we can express T in terms of Mg and θ:
T=Mgcos(θ)(4)
6. Equate the Two Expressions for T:
- Set equations (3) and (4) equal to each other:
Fsin(θ)=Mgcos(θ)
7. Rearranging to Find Tension:
- Cross-multiply to isolate T:
T=Fcos(θ)sin(θ)=Fcot(θ)
8. Final Expression for Tension:
- Thus, the tension T in the string is given by:
T=Fsin(θ)
- Start by drawing the mass M suspended from a rigid support by a rope.
- Indicate the angle θ that the rope makes with the vertical.
- Mark the weight of the mass acting downward as W=Mg (where g is the acceleration due to gravity).
- Indicate the horizontal force F acting on the mass.
- The tension T in the rope acts along the rope at an angle θ from the vertical.
- The weight W acts downward.
- The horizontal force F acts to the right.
- The tension T can be resolved into two components:
- Vertical component: Tcos(θ) (acting upward)
- Horizontal component: Tsin(θ) (acting horizontally)
- Since the mass is in equilibrium, the sum of the forces in both the vertical and horizontal directions must be zero.
- For vertical forces:
Tcos(θ)=Mg(1)
- For horizontal forces:
Tsin(θ)=F(2)
- From equation (2), we can express T in terms of F and θ:
T=Fsin(θ)(3)
- From equation (1), we can express T in terms of Mg and θ:
T=Mgcos(θ)(4)
- Set equations (3) and (4) equal to each other:
Fsin(θ)=Mgcos(θ)
- Cross-multiply to isolate T:
T=Fcos(θ)sin(θ)=Fcot(θ)
- Thus, the tension T in the string is given by:
T=Fsin(θ)
Similar Questions
A mass M is suspended by a rope from a rigid support at A as shown in figure. Another rupe is tied at the end B, and it is pulled horizontally with a force. If the rope AB makes an angle θ with the vertical in equilibrium then the tension in the string AB is
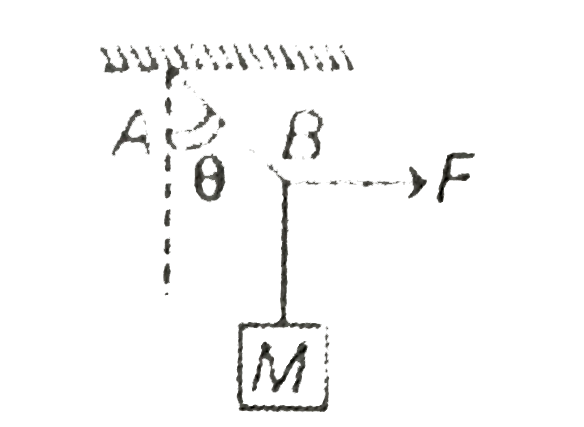
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle '/theta' with the vertical in equilibrium. Then the tension in the string is :
View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA heavy rope is suspended from a rigid support A wave pulse is set up at the lower end, then
View SolutionA mass of 6 kg is suspended by a rope of length 2m from a celling. A force of 50N is applied in horizontal direction at the mid point of the rope. What is the angle of the rope with the verticle in equilibrium:-
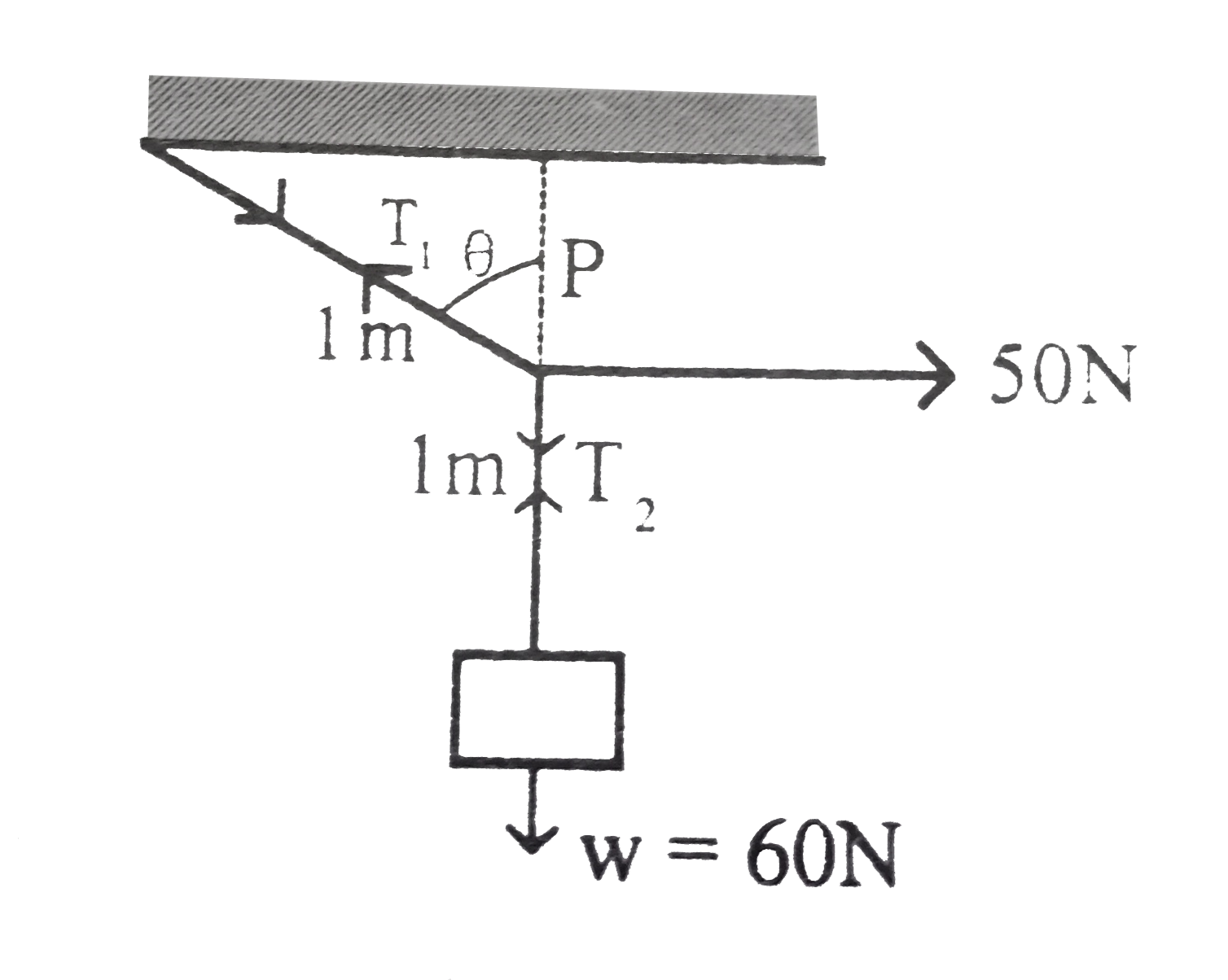
View SolutionSee Fig 5.8 .A mass of 6 kg is suspended by a rope of length 2m from the ceiling . A force of 50 N in the horizontal direction is applied at the mid-point P of the rope, as shown. What is the angle the rope makes with the vertical in equilibrium ? (Take g = 10 m s−2). Neglect the mass of the rope.
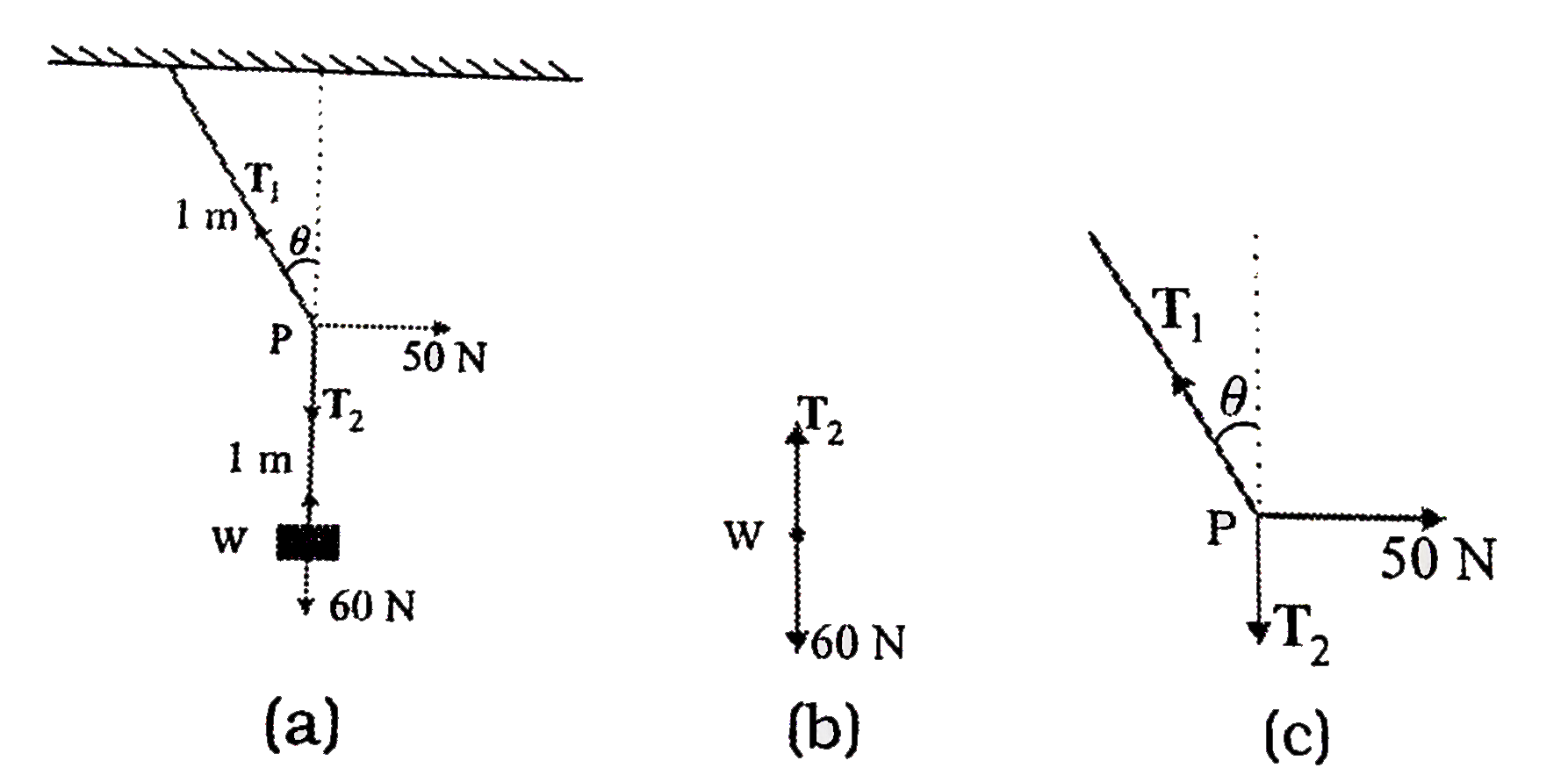
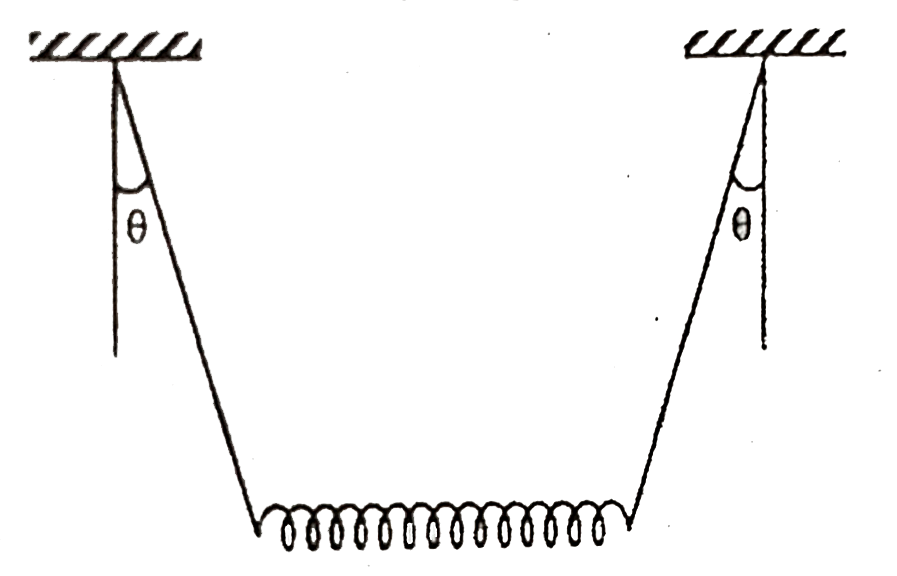
View SolutionA spring of weight W and force constant k is suspended is a horizontal position by tw3o ligth strings attached to its two ends. Each string makes an angle θ with the vertical. The extension of the spring is.
View SolutionA body of mass 10 kg is suspended by a string and is pulled a side with a horizontal force of 49 N. Find the tension in the string, if the body is in equilibrium under these forces.
View Solution
