A body is projected up along an inclined plane from the bottom with speed V1. If it reaches the bottom of the plane with a velocity V2, find (v1/v2) if θ is the angle of inclination with the horizontal and μ be the coefficient of.
sinθ+μcosθsinθ−μcosθ
√si∈θ+μcosθsinθ−μcosθ
cosθ+μsinθcosθ−μsinθ
√cosθ+μsinθcosθ−μsinθ
The correct Answer is:B
To solve the problem, we need to analyze the motion of a body projected up an inclined plane and then descending back down. We will derive the relationship between the initial velocity V1 and the final velocity V2 when the body reaches the bottom of the incline.
Step 1: Analyze the forces acting on the body when projected upwards
When the body is projected upwards along the inclined plane, the forces acting on it are:
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting down the incline: f=μN=μmgcosθ
The net force acting on the body while moving upwards is:
Fnet, up=−mgsinθ−μmgcosθ
This can be expressed as:
Fnet, up=−mg(sinθ+μcosθ)
Step 2: Calculate the acceleration while moving upwards
Using Newton's second law, we can write:
ma=−mg(sinθ+μcosθ)
Dividing both sides by m:
a=−g(sinθ+μcosθ)
Step 3: Apply the equations of motion
Using the equation of motion v2=u2+2as, where:
- v=0 (final velocity at the highest point)
- u=V1 (initial velocity)
- a=−g(sinθ+μcosθ)
- s is the distance traveled up the incline
We have:
0=V21−2g(sinθ+μcosθ)s
Rearranging gives:
V21=2g(sinθ+μcosθ)s(1)
Step 4: Analyze the forces acting on the body when descending
When the body is descending, the forces acting on it are:
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting up the incline: f=μmgcosθ
The net force acting on the body while moving downwards is:
Fnet, down=mgsinθ−μmgcosθ
This can be expressed as:
Fnet, down=mg(sinθ−μcosθ)
Step 5: Calculate the acceleration while moving downwards
Using Newton's second law, we can write:
ma=mg(sinθ−μcosθ)
Dividing both sides by m:
a=g(sinθ−μcosθ)
Step 6: Apply the equations of motion for descending
Using the equation of motion v2=u2+2as, where:
- v=V2 (final velocity)
- u=0 (initial velocity at the bottom)
- a=g(sinθ−μcosθ)
- s is the distance traveled down the incline
We have:
V22=0+2g(sinθ−μcosθ)s
Rearranging gives:
V22=2g(sinθ−μcosθ)s(2)
Step 7: Find the ratio V1V2
From equations (1) and (2), we can find the ratio:
V21V22=2g(sinθ+μcosθ)s2g(sinθ−μcosθ)s
The 2g and s cancel out:
V21V22=sinθ+μcosθsinθ−μcosθ
Taking the square root gives:
V1V2=√sinθ+μcosθsinθ−μcosθ
Final Answer
V1V2=√sinθ+μcosθsinθ−μcosθ
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting down the incline: f=μN=μmgcosθ
Fnet, up=−mgsinθ−μmgcosθ
This can be expressed as:
Fnet, up=−mg(sinθ+μcosθ)
ma=−mg(sinθ+μcosθ)
Dividing both sides by m:
a=−g(sinθ+μcosθ)
- v=0 (final velocity at the highest point)
- u=V1 (initial velocity)
- a=−g(sinθ+μcosθ)
- s is the distance traveled up the incline
0=V21−2g(sinθ+μcosθ)s
Rearranging gives:
V21=2g(sinθ+μcosθ)s(1)
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting up the incline: f=μmgcosθ
Fnet, down=mgsinθ−μmgcosθ
This can be expressed as:
Fnet, down=mg(sinθ−μcosθ)
ma=mg(sinθ−μcosθ)
Dividing both sides by m:
a=g(sinθ−μcosθ)
- v=V2 (final velocity)
- u=0 (initial velocity at the bottom)
- a=g(sinθ−μcosθ)
- s is the distance traveled down the incline
V22=0+2g(sinθ−μcosθ)s
Rearranging gives:
V22=2g(sinθ−μcosθ)s(2)
V21V22=2g(sinθ+μcosθ)s2g(sinθ−μcosθ)s
The 2g and s cancel out:
V21V22=sinθ+μcosθsinθ−μcosθ
V1V2=√sinθ+μcosθsinθ−μcosθ
V1V2=√sinθ+μcosθsinθ−μcosθ
Similar Questions
A body is projected up along the rough inclined plane from the bottom with some velocity. It travels up the incline and then returns back. If the time of ascent is ta and time of descent is td then
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA block is kept on an inclined plane of inclination θ of length l. the velocity of particle at the bottom of inclined is (the coefficient of friciton is μ)
View SolutionA solid sphere is projected up along an inclined plank of inclination θ=30∘ with a speed v=2ms−1. If it rolls without slipping find the maximum distance traversed by it (g=10ms−2)
View SolutionA disc rolls down a plane of length L and inclined at angle θ, without slipping. Its velocity on reaching the bottom will be :-
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View SolutionA small disc is released from rest at A on an inclined plane AB so that it rolls down without slipping. It reaches the bottom with linear velocity v1 in time t1. Next a small ring released form rest on the inclined plane AC so that it rolls down without slipping. It reaches the bottom with linear vlocity v2 in time t2. Given θ1=30∘,θ2=60∘, and h=10m. Then,
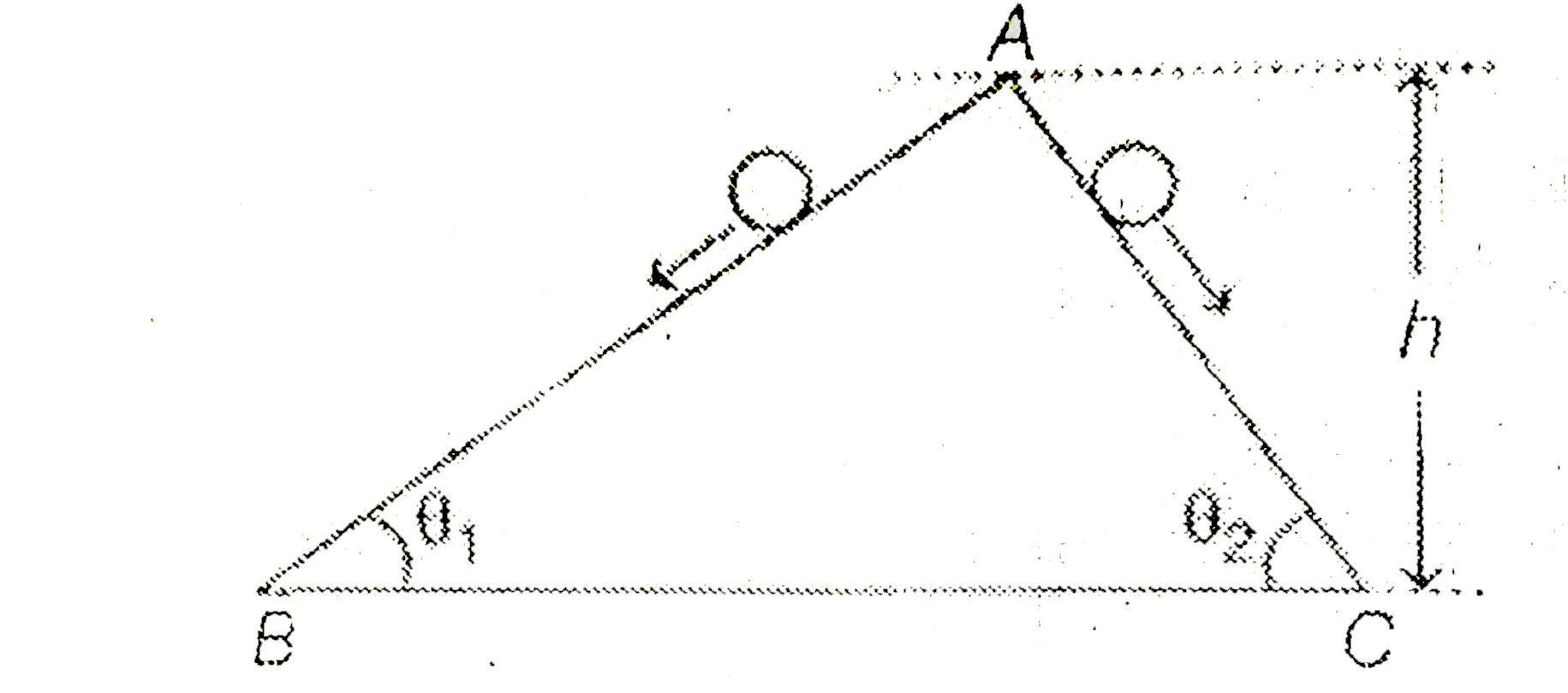
View SolutionA block is kept on a inclined plane of inclination θ of length l. The velocity of particle at the bottom of inclined is (the coefficient of friction is μ
View SolutionAt what angle should a ball be projected up an inclined plane with a velocity v0 so that it may hit the incline normally. The angle of the inclined plane with the horizontal is ∝.
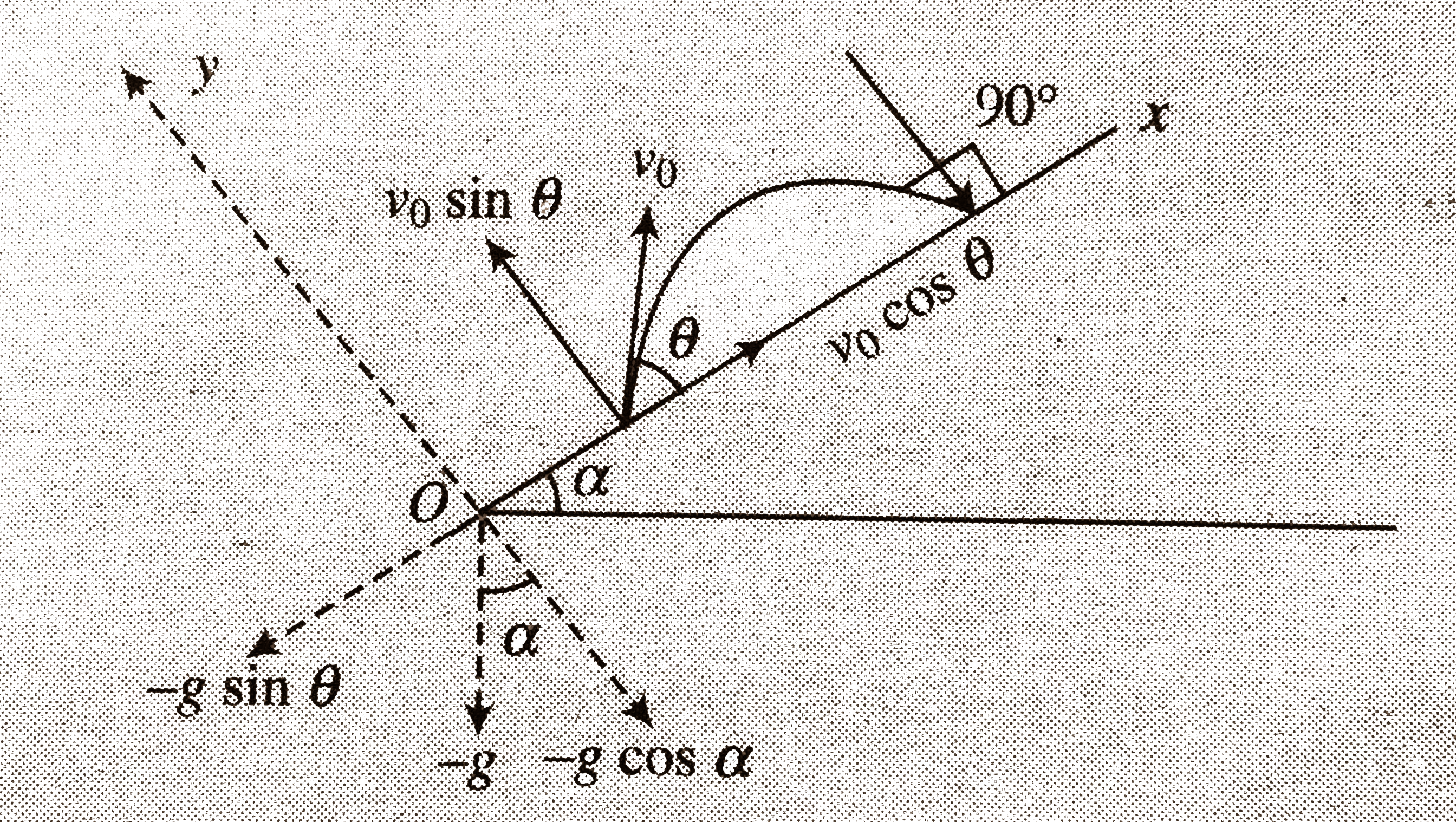 .
.
View SolutionAn object of mass m is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
View Solution
