There is a small hole in a table. A string of length lm passes through it. Two bodies of masses 70g and 100 g are attached at its ends. The lOOg mass hangs freely at a depth of 60 cm from the table. If this mass is to be in equilibrium, the other mass should rotate in a circle with a frequency equal to
(4π/140) Hz
π/140Hz
π/√140 Hz
√1404πHz
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the two masses and apply the concepts of circular motion and equilibrium.
Step 1: Identify the given values
- Mass m1=70g=0.07kg
- Mass m2=100g=0.1kg
- Total length of the string L=1m
- Length of the hanging part Lh=60cm=0.6m
Step 2: Calculate the radius of the circular motion
The length of the string that rotates in a circle is given by:
r=L−Lh=1m−0.6m=0.4m
Step 3: Analyze the forces acting on the hanging mass m2
The forces acting on mass m2 are:
- Weight W=m2g=0.1kg×10m/s2=1N
- Tension T in the string
For the system to be in equilibrium:
T=m2g=1N
Step 4: Analyze the forces acting on the rotating mass m1
For mass m1 which is rotating in a circle, the tension T also provides the centripetal force required for circular motion:
T=m1v2r
Substituting T=1N:
1=0.07v20.4
Step 5: Solve for the velocity v
Rearranging the equation gives:
v2=1×0.40.07
v2=0.40.07≈5.7143
v=√5.7143≈2.39m/s
Step 6: Relate linear velocity to angular frequency
The relationship between linear velocity v and angular frequency ω is given by:
v=rω⟹ω=vr
Substituting the values:
ω=2.390.4≈5.975rad/s
Step 7: Calculate the frequency f
The frequency f is related to angular frequency ω by:
f=ω2π
Substituting the value of ω:
f=5.9752π≈5.9756.2832≈0.951Hz
Final Answer
The frequency of rotation of the smaller mass m1 for the system to be in equilibrium is approximately 0.951Hz.
---
- Mass m1=70g=0.07kg
- Mass m2=100g=0.1kg
- Total length of the string L=1m
- Length of the hanging part Lh=60cm=0.6m
The length of the string that rotates in a circle is given by:
r=L−Lh=1m−0.6m=0.4m
The forces acting on mass m2 are:
- Weight W=m2g=0.1kg×10m/s2=1N
- Tension T in the string
T=m2g=1N
For mass m1 which is rotating in a circle, the tension T also provides the centripetal force required for circular motion:
T=m1v2r
Substituting T=1N:
1=0.07v20.4
Rearranging the equation gives:
v2=1×0.40.07
v2=0.40.07≈5.7143
v=√5.7143≈2.39m/s
The relationship between linear velocity v and angular frequency ω is given by:
v=rω⟹ω=vr
Substituting the values:
ω=2.390.4≈5.975rad/s
The frequency f is related to angular frequency ω by:
f=ω2π
Substituting the value of ω:
f=5.9752π≈5.9756.2832≈0.951Hz
The frequency of rotation of the smaller mass m1 for the system to be in equilibrium is approximately 0.951Hz.
Similar Questions
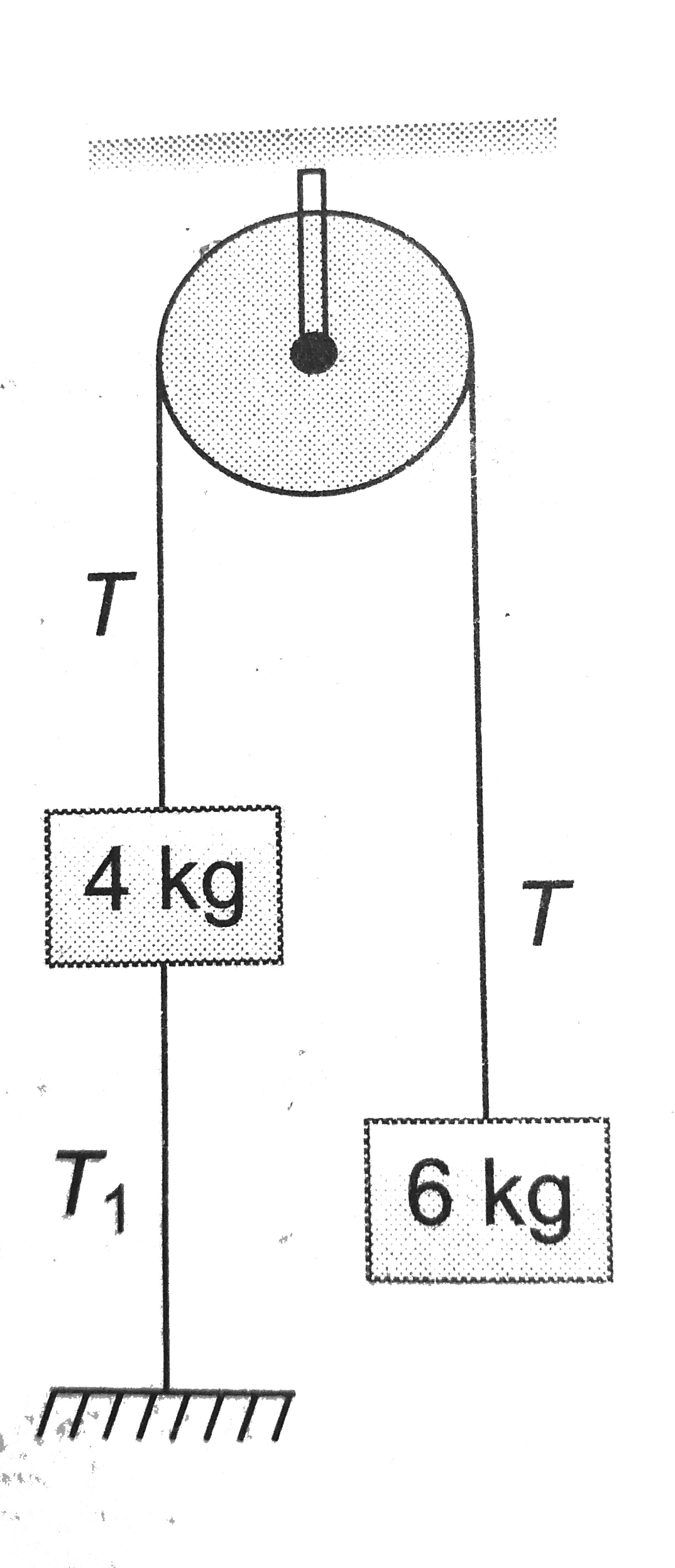
Two bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution
Knowledge Check
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2A uniform chain of length 2m is kept on a table such that a length of 60cm hangs freely from the edge of the table . The total mass of the chain is 4kg What is the work done in pulling the entire the chain the on the table ?
A12.9JB6.3 JC3.6 JD2.0 J
A particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View SolutionA uniform chain of mass 4 kg and length 2 m is kept on table such that 3/10th of the chain hanges freely from the edge of the table. How much work has to be done in pulling the entire chain on the table?
View SolutionA string of length 0.1 m cannot bear a tension more than 100 N. It is lied to a body of mass 100 g and rotated in a horizontal circle. The maximum angular velocity can be
View SolutionA body of mass 20 kg is resting on a table. A light string is attached to it and passed over a smooth pulley at the edge of the table and a mass 3kg is attached at the free end. What is the acceleration of the system of the coefficient of kinetic friction between the mass and the table is 0.04 ? What is the tension in the string ?
View SolutionA uniform chain of length 4m is kept on a table such that a length of 120 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg What is the work done in pulling the entire chain on the table ?
View Solution
