A string of length L consists of two distinct sections. The left half has linear mass density while the right half has linear mass density . Tension in the string is . The time required for a transverse wave pulse to travel from one end of the string to the other is
The correct Answer is:D
To solve the problem, we need to calculate the time required for a transverse wave pulse to travel from one end of the string to the other, considering the two different sections of the string with distinct linear mass densities.
1. Identify the Sections of the String:
- The string is divided into two halves:
- Left half (length = L/2) with linear mass density μ1=μ02
- Right half (length = L/2) with linear mass density μ2=3μ0
2. Calculate the Wave Velocity in Each Section:
- The velocity of a transverse wave in a string is given by:
v=√Tμ
- For the left half:
vL=√F0μ1=
⎷F0μ02=√2F0μ0
- For the right half:
vR=√F0μ2=√F03μ0=√F03μ0
3. Calculate the Time Taken to Travel Each Section:
- The time taken for the wave to travel from the left end to the midpoint (left half):
tL=DistanceVelocity=L2vL=L2√2F0μ0=L2⋅√μ02F0=L2⋅√μ0√2F0
- The time taken for the wave to travel from the midpoint to the right end (right half):
tR=DistanceVelocity=L2vR=L2√F03μ0=L2⋅√3μ0F0=L2⋅√3μ0√F0
4. Total Time Calculation:
- The total time t for the wave to travel from one end of the string to the other is the sum of the two times:
t=tL+tR
- Substituting the values:
t=L2⋅√μ0√2F0+L2⋅√3μ0√F0
- Factor out L2:
t=L2(√μ0√2F0+√3μ0√F0)
- Simplifying further:
t=L2(√μ0√2F0+√3μ0⋅√2√2F0)=L2√2F0(√μ0+√6μ0)
- This gives:
t=L2√2F0√μ0(1+√6)
Final Answer:
The time required for a transverse wave pulse to travel from one end of the string to the other is:
t=L2√2F0√μ0(1+√6)
- The string is divided into two halves:
- Left half (length = L/2) with linear mass density μ1=μ02
- Right half (length = L/2) with linear mass density μ2=3μ0
- The velocity of a transverse wave in a string is given by:
v=√Tμ
- For the left half:
vL=√F0μ1=
⎷F0μ02=√2F0μ0
- For the right half:
vR=√F0μ2=√F03μ0=√F03μ0
- The time taken for the wave to travel from the left end to the midpoint (left half):
tL=DistanceVelocity=L2vL=L2√2F0μ0=L2⋅√μ02F0=L2⋅√μ0√2F0
tR=DistanceVelocity=L2vR=L2√F03μ0=L2⋅√3μ0F0=L2⋅√3μ0√F0
- The total time t for the wave to travel from one end of the string to the other is the sum of the two times:
t=tL+tR
- Substituting the values:
t=L2⋅√μ0√2F0+L2⋅√3μ0√F0
- Factor out L2:
t=L2(√μ0√2F0+√3μ0√F0)
- Simplifying further:
t=L2(√μ0√2F0+√3μ0⋅√2√2F0)=L2√2F0(√μ0+√6μ0)
- This gives:
t=L2√2F0√μ0(1+√6)
The time required for a transverse wave pulse to travel from one end of the string to the other is:
t=L2√2F0√μ0(1+√6)
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
4 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
4 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
4 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
Three pieces of string, each of length L, are joined together end-to-end, to make a combined string of length 3L. The first piece of string has mass per unit length μ1, the second piece has mass per unit length μ2=4μ1 and the third piece has mass per unit length μ3=μ1/4 .
(a) If the combined string is under tension F, how much time does it take a transverse wave to travel the entire length 3L? Give your answer in terms of L,F and μ1 .
(b) Does your answer to part (a) depend on the order in which the three piece are joined together? Explain.
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F. Find the time taken by wave to reach from source end to fixed end.

View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F.

Find the ratio of wavelength of the wave on four string, starting from right hand side.
View SolutionFigure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
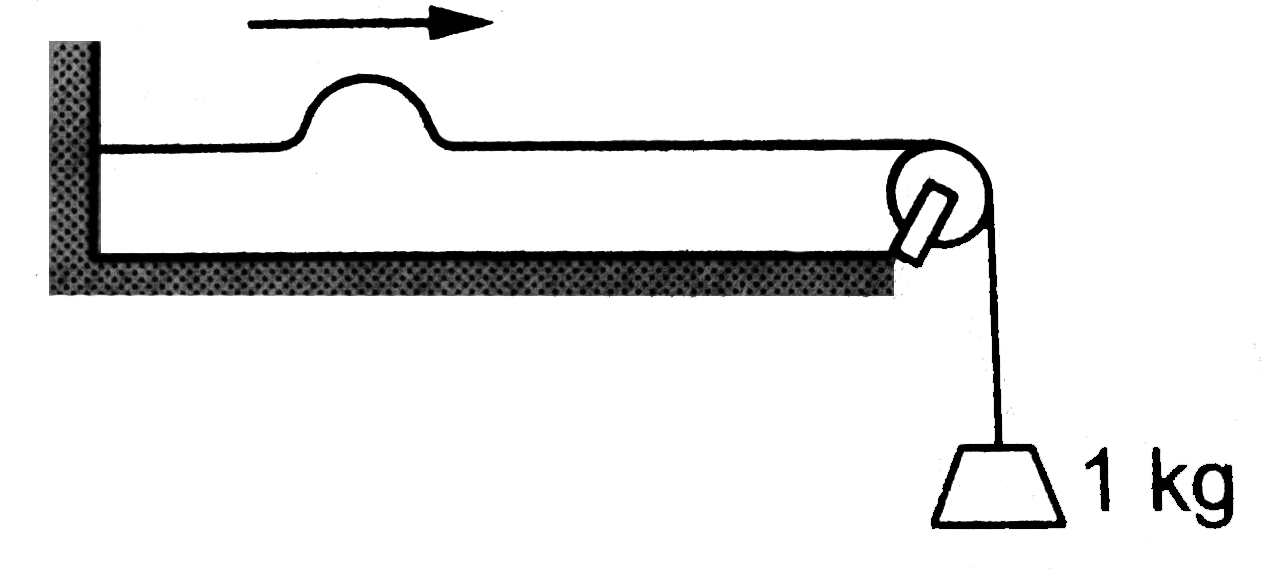
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View Solutionthe linear density of a wire under tension t varies linearly from μ1 to μ20.Calculate the time that a pulse would need to pass one to the other.The length of the wire is l
View SolutionOne end of a string of length L is tied to the ceiling of a lift accelerating upwards with an acceleration 2g. The other end o the string is free. The linear mass density of the string varies linearly from 0 to λ from bottom to top. The acceleration of a wave pulled through out the string is pg4. Find p.
View SolutionFigure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
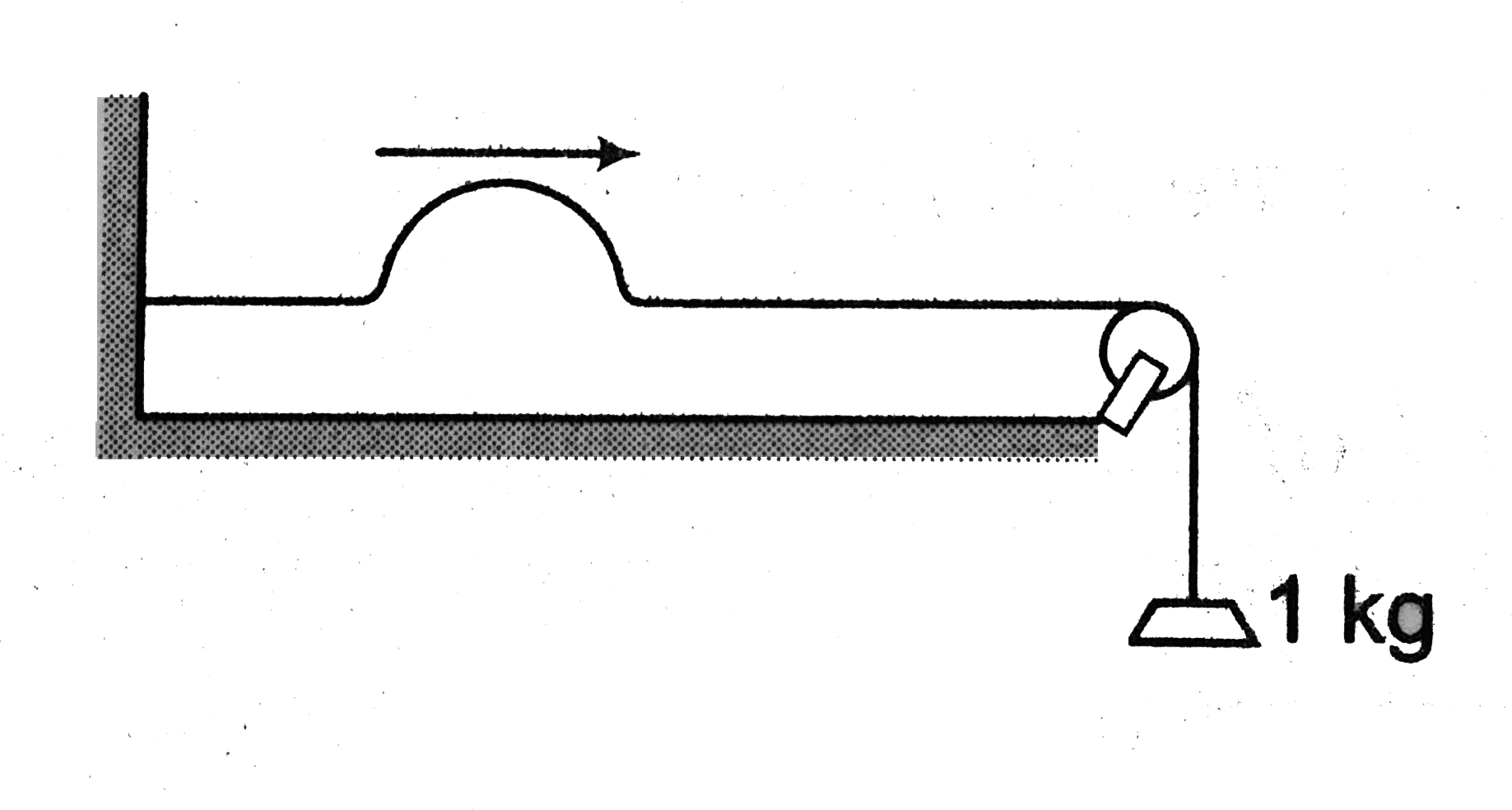
View Solution
