One end of a string of length L is tied to the ceiling of a lift accelerating upwards with an acceleration 2g. The other end o the string is free. The linear mass density of the string varies linearly from 0 to λ from bottom to top. The acceleration of a wave pulled through out the string is pg4. Find p.
The correct Answer is:3
To solve the problem step by step, we will analyze the situation involving the string in the lift and derive the necessary equations to find the value of p.
Step 1: Understand the Setup
We have a string of length L tied to the ceiling of a lift that is accelerating upwards with an acceleration of 2g. The linear mass density of the string varies linearly from 0 at the bottom to λ at the top.
Step 2: Define the Linear Mass Density
The linear mass density μ(y) at a distance y from the bottom of the string can be expressed as:
μ(y)=λLy
where y varies from 0 (bottom) to L (top).
Step 3: Calculate the Mass of a Small Element
Consider a small element of the string of length dy at a height y. The mass dm of this element is given by:
dm=μ(y)⋅dy=(λLy)dy
Step 4: Calculate the Total Mass of the Element
To find the total mass m(y) of the string from the bottom to height y, we integrate:
m(y)=∫y0μ(y′)dy′=∫y0(λLy′)dy′=λL∫y0y′dy′=λL⋅y22=λy22L
Step 5: Analyze Forces on the Element
The tension T in the string at height y must balance the weight of the mass below it and provide the necessary force for the upward acceleration of 2g:
T−m(y)g=m(y)⋅(2g)
Substituting m(y):
T−(λy22L)g=(λy22L)⋅(2g)
This simplifies to:
T=3(λy22L)g
Step 6: Calculate Wave Velocity
The velocity v of a wave on the string is given by:
v=√Tμ(y)
Substituting T and μ(y):
v=
⎷3(λy22L)gλLy=√3gy2
Step 7: Relate Wave Velocity to Acceleration
From the problem, we know that the acceleration of the wave is given as pg4. The wave acceleration can also be expressed in terms of the wave velocity:
a=d(v2)dy=ddy(3gy2)=3g2
Step 8: Equate the Two Expressions for Acceleration
Setting the two expressions for acceleration equal gives:
3g2=pg4
Dividing both sides by g (assuming g≠0):
32=p4
Step 9: Solve for p
Multiplying both sides by 4:
p=6
Final Answer
Thus, the value of p is:
6
We have a string of length L tied to the ceiling of a lift that is accelerating upwards with an acceleration of 2g. The linear mass density of the string varies linearly from 0 at the bottom to λ at the top.
The linear mass density μ(y) at a distance y from the bottom of the string can be expressed as:
μ(y)=λLy
where y varies from 0 (bottom) to L (top).
Consider a small element of the string of length dy at a height y. The mass dm of this element is given by:
dm=μ(y)⋅dy=(λLy)dy
To find the total mass m(y) of the string from the bottom to height y, we integrate:
m(y)=∫y0μ(y′)dy′=∫y0(λLy′)dy′=λL∫y0y′dy′=λL⋅y22=λy22L
The tension T in the string at height y must balance the weight of the mass below it and provide the necessary force for the upward acceleration of 2g:
T−m(y)g=m(y)⋅(2g)
Substituting m(y):
T−(λy22L)g=(λy22L)⋅(2g)
This simplifies to:
T=3(λy22L)g
The velocity v of a wave on the string is given by:
v=√Tμ(y)
Substituting T and μ(y):
v=
⎷3(λy22L)gλLy=√3gy2
From the problem, we know that the acceleration of the wave is given as pg4. The wave acceleration can also be expressed in terms of the wave velocity:
a=d(v2)dy=ddy(3gy2)=3g2
Setting the two expressions for acceleration equal gives:
3g2=pg4
Dividing both sides by g (assuming g≠0):
32=p4
Multiplying both sides by 4:
p=6
Thus, the value of p is:
6
Topper's Solved these Questions
- WAVE MOTIONBook:DC PANDEY ENGLISHChapter:WAVE MOTIONExercise:Matrix Matching
Explore 16 Videos
- VECTORSBook:DC PANDEY ENGLISHChapter:VECTORSExercise:Medical enrances gallery
Explore 9 Videos
- WORK, ENERGY & POWERBook:DC PANDEY ENGLISHChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
Similar Questions
One end of a string of length L is tied to the celling of lift accelerating upwards with an accelerating 2g The other end of the string is free. The linear mass density of the string varies linearly from 0 of λ from bottom to top :-
View SolutionOne end of a string of length L is tied to the ceiling of a lift acceleration upwards with an acceleration 2g. The other end of the string is free. The linear mass density of the string varies linearly from 0→λ from bottom to top. Choose the correct option(s)
View SolutionA pendulum is hanging from the ceiling of a car having an acceleration a0 with respect to the road. Find the angle made by the string with the vertical.
View SolutionA body of mass M is hanging by an inextensible string of mass m. If the free end of the string accelerates up with constant acceleration a. find the variation of tension in the string a function of the distance measured from the mass M (bottom of the string).

View SolutionThe acceleration of the 2 kg block if the free end of string is pulled with a force of 20 N as shown is
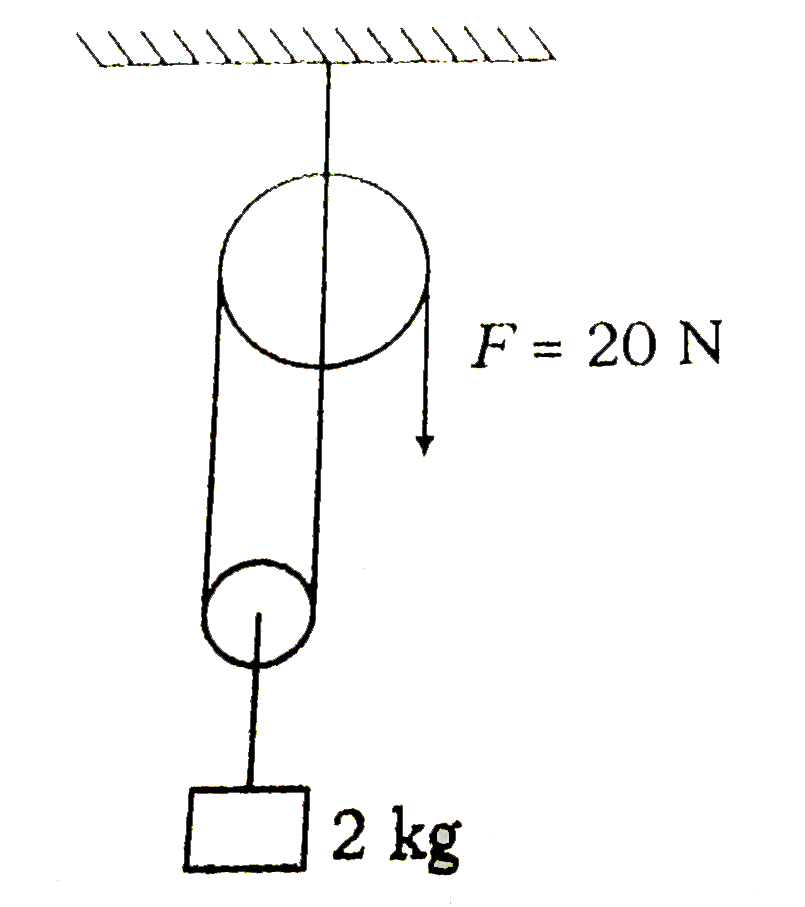
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View Solution
In the shown mass pulley system, pulleys and string are massless. The one end of the string is pulleed by the force F=2mg. The acceleration of the block will be
View SolutionOn the surface of a solid cylinder of mass 2 kg and radius 25 cm a string is wound several times and the end of the string is held stationary while the cylinder is released from rest. What is the acceleration of the cylinder and the tension in the string ?
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View Solution