In which case is the power being delivered by a given progressive sinusoidal wave on a given string is doubled? Material of the string is unchanged.
The wave amplitude is doubled (keeping the frequency the same).
The wave frequency is cut in half (keeping the amplitude the same).
Tension in the string is made four times the initial value (keeping its linear density, amplitude and frequency the same).
The diameter of the string is doubled (keeping the tension amplitude and frequency the same).
The correct Answer is:C, D
To determine in which case the power delivered by a given progressive sinusoidal wave on a string is doubled, we need to analyze the relationship between power, amplitude, frequency, tension, and linear density of the string. The power P transmitted by a wave on a string can be expressed as:
P=12μω2A2v
Where:
- μ is the linear density of the string (mass per unit length),
- ω is the angular frequency of the wave,
- A is the amplitude of the wave,
- v is the wave speed on the string.
The wave speed v can be expressed in terms of tension T and linear density μ:
v=√Tμ
1. Identify the parameters affecting power:
The power delivered by the wave depends on amplitude A, frequency (via angular frequency ω), tension T, and linear density μ.
2. Case 1 - Doubling the amplitude:
If the amplitude A is doubled (i.e., A=2A0), the power becomes:
P′=12μω2(2A0)2v=12μω2(4A20)v=4P0
This quadruples the power, not doubles it.
3. Case 2 - Halving the frequency:
If the frequency is cut in half, then ω=12ω0:
P′=12μ(12ω0)2A20v=12μ14ω20A20v=18P0
This reduces the power, not doubles it.
4. Case 3 - Increasing tension:
If the tension T is made four times the initial value (i.e., T=4T0), the wave speed becomes:
v=√4T0μ=2√T0μ=2v0
Thus, the power becomes:
P′=12μω2A20(2v0)=2P0
This doubles the power.
5. Case 4 - Doubling the diameter:
If the diameter of the string is doubled, the linear density μ increases (since μ is proportional to the cross-sectional area, which is proportional to the square of the diameter). The new linear density becomes:
μ′=4μ0
The power becomes:
P′=12(4μ0)ω2A20v
This increases the power by a factor of 4, not doubles it.
Conclusion:
The only case in which the power delivered by the wave is doubled is when the tension in the string is made four times its initial value while keeping the linear density, amplitude, and frequency the same.
- μ is the linear density of the string (mass per unit length),
- ω is the angular frequency of the wave,
- A is the amplitude of the wave,
- v is the wave speed on the string.
The power delivered by the wave depends on amplitude A, frequency (via angular frequency ω), tension T, and linear density μ.
If the amplitude A is doubled (i.e., A=2A0), the power becomes:
P′=12μω2(2A0)2v=12μω2(4A20)v=4P0
This quadruples the power, not doubles it.
If the frequency is cut in half, then ω=12ω0:
P′=12μ(12ω0)2A20v=12μ14ω20A20v=18P0
This reduces the power, not doubles it.
If the tension T is made four times the initial value (i.e., T=4T0), the wave speed becomes:
v=√4T0μ=2√T0μ=2v0
Thus, the power becomes:
P′=12μω2A20(2v0)=2P0
This doubles the power.
If the diameter of the string is doubled, the linear density μ increases (since μ is proportional to the cross-sectional area, which is proportional to the square of the diameter). The new linear density becomes:
μ′=4μ0
The power becomes:
P′=12(4μ0)ω2A20v
This increases the power by a factor of 4, not doubles it.
The only case in which the power delivered by the wave is doubled is when the tension in the string is made four times its initial value while keeping the linear density, amplitude, and frequency the same.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-III (LEVEL-II(ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))3videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-III (LEVEL-II(ADVANCED) MATRIX MATCHING TYPE QUESTIONS))1videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-III (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))7videos
WAVE MOTION
- BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -366videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)97videos
WAVE MOTION AND SOUND
Similar Questions
Knowledge Check
- Question 1 - Select One
Figure shows a sinusoidal wave at a given instant.
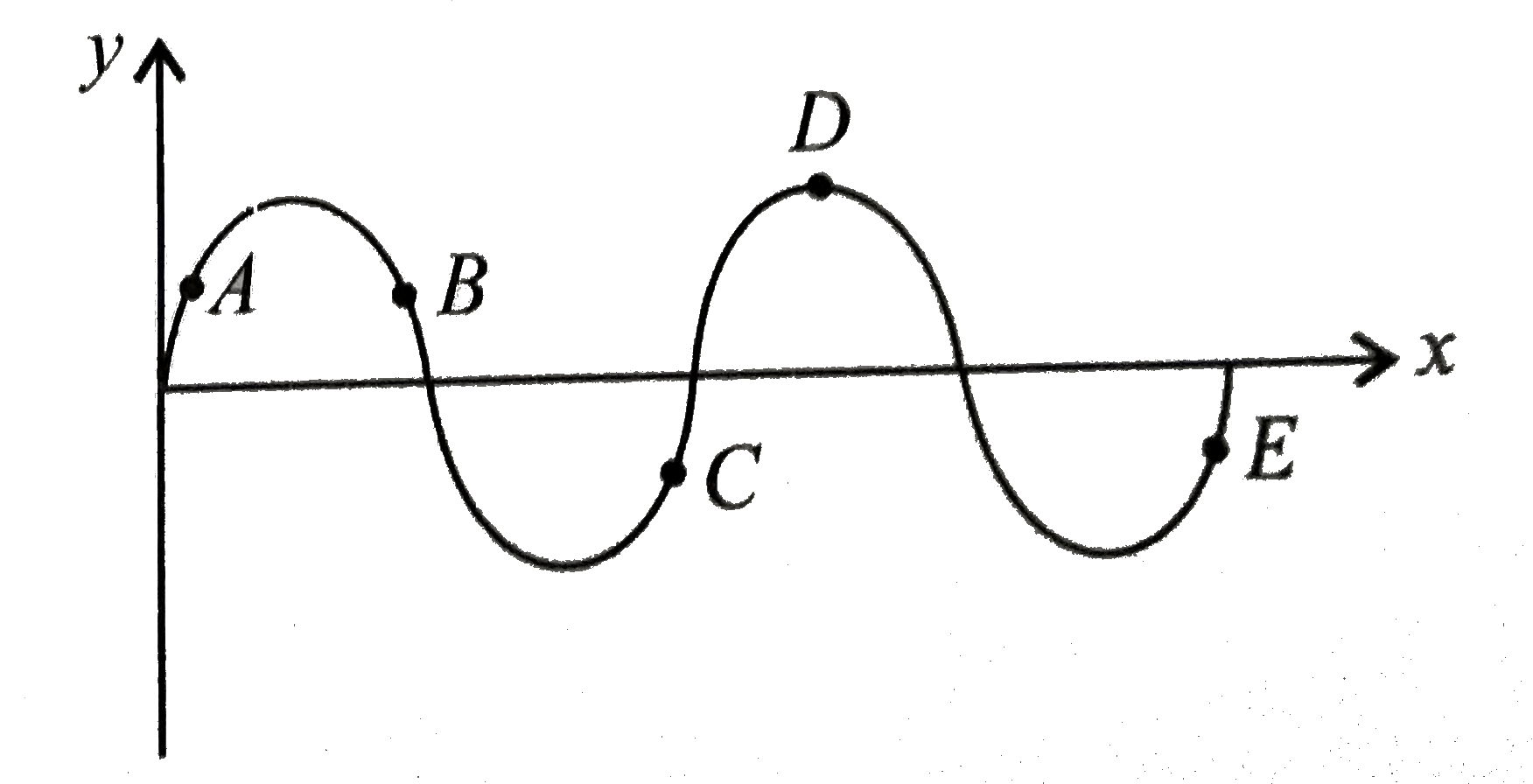
Which points are in phase?AA,BBB,CCB,DDC,E
A harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
View SolutionSinusoidal waves 5.00 cm in amplitude are to be transmitted along a string having a linear mass density equal to 4.00×10−2kg/m.If the source can deliver a average power of 90 W and the string is under a tension of 100 N, then the highest frequency at which the source can operate is (take π2=10):
View SolutionIn each of the four situations of column-I , a stretched string or an organ pipe is given along with the required data. In case of strings the tension in string is T=102.4 N and the mass per unit length of string is 1g/m. Speed of sound in air is 320 m/s. Neglect end corrections.The frequencies of resonance are given in column-II.Match each situation in column-I with the possible resonance frequencies given in Column-II.
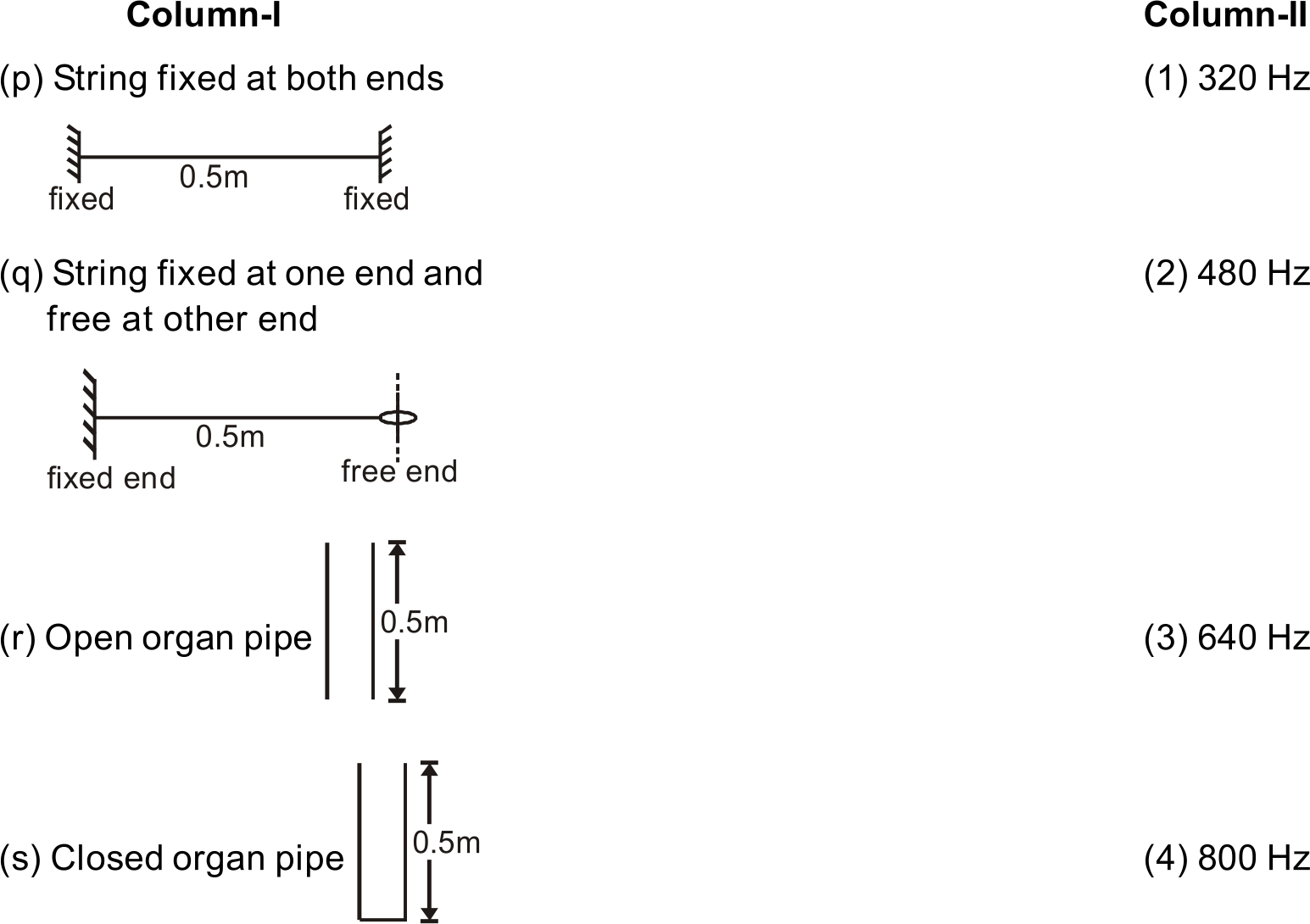 View Solution
View SolutionIn AM wave total power of side bands is given by :
View SolutionThree resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies ? (c) Which overtones are these frequencies ? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string ?
View SolutionThree resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies ? (c) Which overtones are these frequencies ? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string ?
View SolutionA harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four times that of the first string, and that the boundary between the two strings is at x=0. If the expression for the incident wave is
yi=Aicos(k1x−ω1t)
(a) What are the expressions for the transmitted and the reflected waves in terms of Ai,k1 and ω1?
(b) Show that the average power carried by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves.View Solution

