A driver in a stationary car horns which produces sound waves having frequency 2000 Hz. The waves are directed normally towards a reflecting wall. If the wall approaches the car with a velocity u = 3.3 m/s. The change in the frequency of sound after reflection from the wall is x%. Then x
The correct Answer is:2
To solve the problem, we need to determine the change in frequency of sound waves after they reflect off a wall that is approaching a stationary source of sound. We will use the Doppler effect formula for sound.
1. Identify the Given Values:
- Frequency of the sound produced by the car (f) = 2000 Hz
- Velocity of the wall (u) = 3.3 m/s
- Speed of sound in air (c) = 340 m/s (standard value)
2. Calculate the Apparent Frequency (f') as the Wall Approaches:
Since the source (the car) is stationary and the wall is moving towards the source, we can use the formula for the apparent frequency when the observer is moving towards a stationary source:
f′=f(c+uc)
Substituting the known values:
f′=2000(340+3.3340)
f′=2000(343.3340)
f′=2000×1.010
f′≈2019.4 Hz
3. Calculate the Change in Frequency:
The change in frequency (Δf) is given by:
Δf=f′−f
Δf=2019.4−2000=19.4 Hz
4. Calculate the Percentage Change in Frequency (x%):
The percentage change in frequency is calculated using the formula:
x=(Δff)×100
Substituting the values:
x=(19.42000)×100
x=0.97%
Final Answer:
The value of x is approximately 0.97%.
- Frequency of the sound produced by the car (f) = 2000 Hz
- Velocity of the wall (u) = 3.3 m/s
- Speed of sound in air (c) = 340 m/s (standard value)
Since the source (the car) is stationary and the wall is moving towards the source, we can use the formula for the apparent frequency when the observer is moving towards a stationary source:
f′=f(c+uc)
Substituting the known values:
f′=2000(340+3.3340)
f′=2000(343.3340)
f′=2000×1.010
f′≈2019.4 Hz
The change in frequency (Δf) is given by:
Δf=f′−f
Δf=2019.4−2000=19.4 Hz
The percentage change in frequency is calculated using the formula:
x=(Δff)×100
Substituting the values:
x=(19.42000)×100
x=0.97%
The value of x is approximately 0.97%.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
A driver in a stationary car blows a horn which produces monochromatic sound waves of freqeuncy 1000 Hz normally towards a reflecting wall. The wall approaches the car with a speed of 3.3ms.
View Solution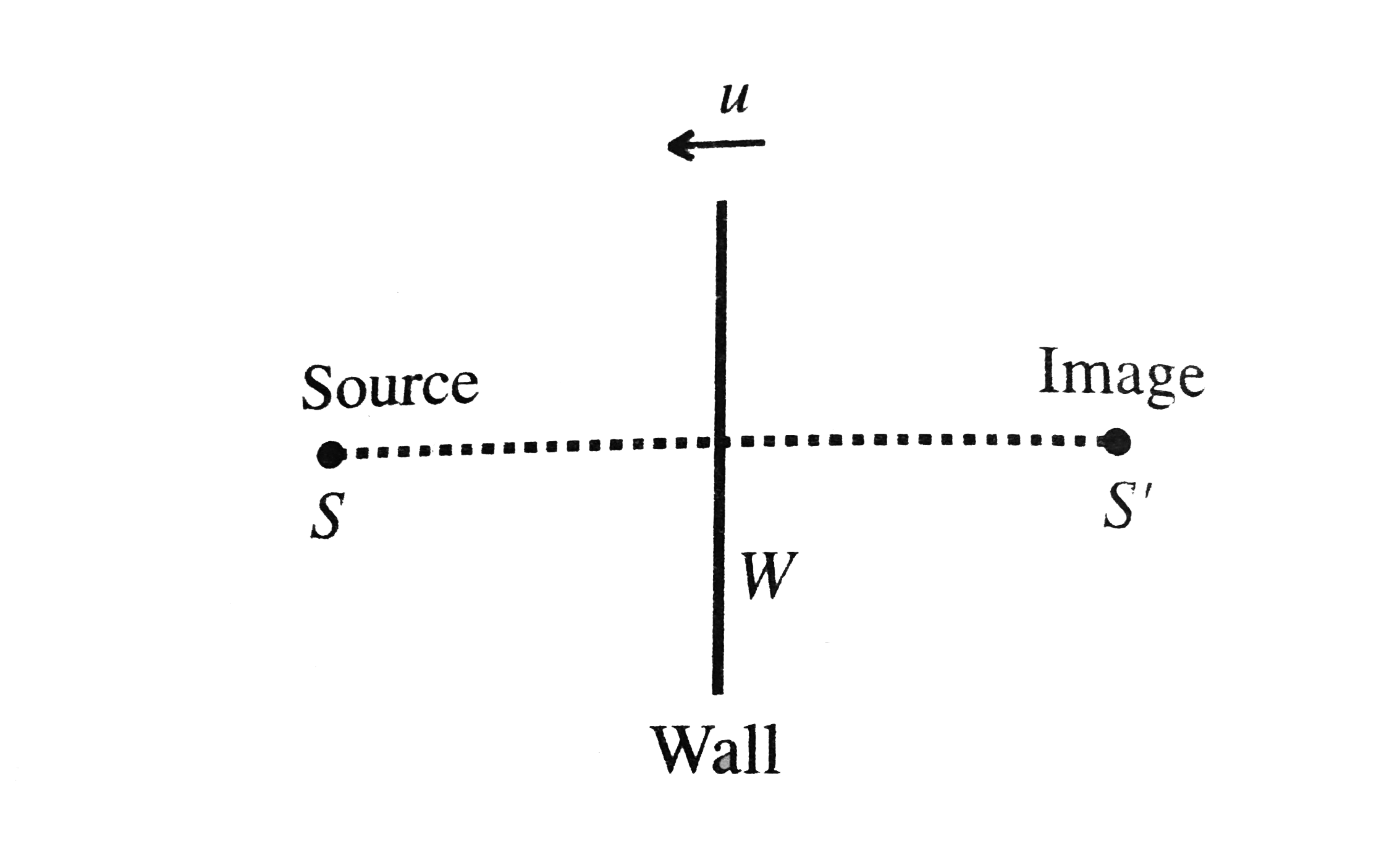 A driver in a stationary car horns which produces monochromatic sound waves of frequency n=1000Hz, normally towards a reflecting wall. If the wall approaches the car will a velocity u=3.3ms, calculate the frequency of sound reflected from wall and heard by the driver. What is the percentage change of sound frequency of reflection from the wall?
A driver in a stationary car horns which produces monochromatic sound waves of frequency n=1000Hz, normally towards a reflecting wall. If the wall approaches the car will a velocity u=3.3ms, calculate the frequency of sound reflected from wall and heard by the driver. What is the percentage change of sound frequency of reflection from the wall?
View SolutionA bat flies perpendicularly towards a wall with a speed of 6 m/s, emitting sound of frequency 450 kHz. What is the frequency of the wave reflected from the wall that it will hear? Given c=340m/s?
View SolutionA bat flies perpendicularly towards a wall with a speed of 6 m/s, emitting sound of frequency 450 kHz. What is the frequency of the wave reflected from the wall that it will hear? Given c=340ms?
View SolutionA bat flies perpendicularly towards a wall with a speed of 6 m/s, emitting sound of frequency 450 kHz. What is the frequency of the wave reflected from the wall that it will hear? Given c=340ms?
View SolutionA stationary sound sound 's' of frequency 334 Hz and a stationary ovserver 'O' are placed near a reflecting suface moving away from the source with velocity 2 m/s as shown in the figure. If the velocity of the sound waves is air is v= 330 m/s the apparent frequency of the echo is
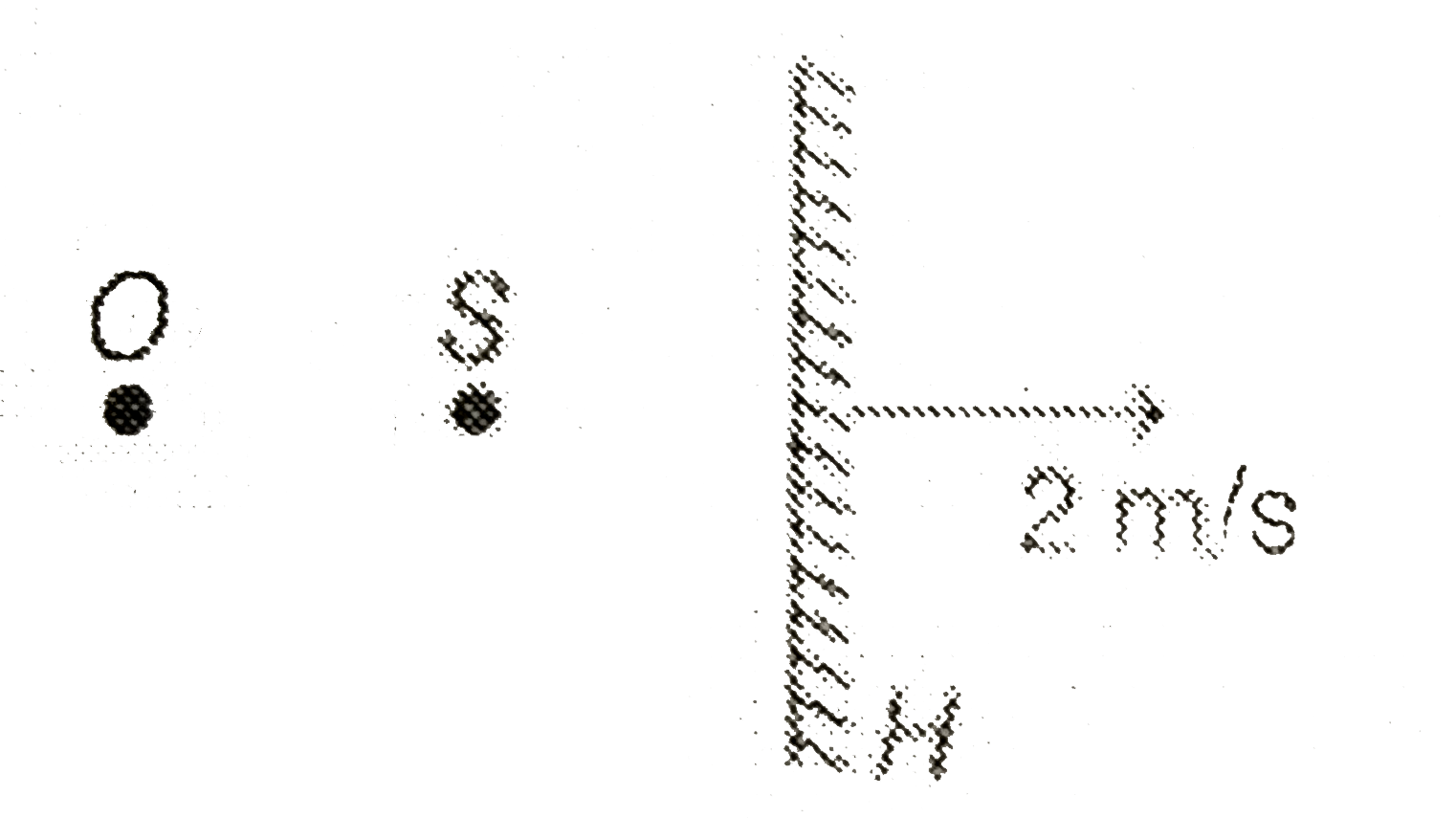
View SolutionSound waves of frequency 660HZ fall normally on perfectly reflecting wall. The distance from the wall at which the air particles have the maximum amplitude of vibration is (speed of sound in air = 330m/s)
View SolutionSound waves of frequency 600HZ fall normally on perfectly reflecting wall. The distance from the wall at which the air particles have the maximum amplitude of vibration is (speed of sound in air = 330m/s)
View SolutionA car travelling towards a hill at 10m/s sound its horn which a frequency 500HZ. This is heard in a second car travelling behind the first car in the same direction with speed 20m/s. The sound can also be heard in the second car by reflections of sound the hill. The beat frequency heard by the driver of the sound car will be (speed of sound in air =340m/s)
View SolutionA car travels at a speed of 'a' towards a high wall. The driver sounds a horn of frequency 'n'. If V is the velocity of sound in air, frequency of reflected sound heard by the driver is
View Solution
